БАНК РЕФЕРАТОВ

Иррациональные уравнения и неравенства

• Иррациональным уравнением (или неравенством) принято называть уравнение (или неравенство), в котором неизвестная величина содержится под знаком радикала. Относящийся к этой теме материал весьма обширен и является неотъемлемой частью вступительного экзамена по математике практически любого высшего учебного заведения. Поэтому необходимо тщательно проработать основные методы решения типовых иррациональных уравнений и неравенств.

При решении простейших иррациональных уравнений придерживайтесь следующих схем.
Уравнение

равносильно системе

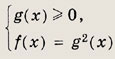
Обращаем внимание на то, что искать область определения данного уравнения, т.е. решать неравенство

в данном случае не нужно. Уравнение

равносильно уравнению без радикала

f(x) = g³(x).

Решите простейшие и сводящиеся к простейшим уравнения (1—22):

Задание 1.

Решение:

Данное уравнение равносильно системе

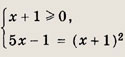
Решаем последнее уравнение; имеем х² - Зх + 2 = 0, откуда х₁ = 1; Х₂ = 2. Оба решения удовлетворяют неравенству х + 1 > 0.

Ответ:

{1; 2}

Задание 2.

Ответ:

2

Задание 3.

Ответ:

2

Задание 4.

Ответ:

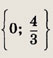
Задание 5.

Ответ:

2

Задание 6.

Ответ:

23

Задание 7.

Ответ:

0

Задание 8.

Решение:

Уравнение равносильно следующему:

9 - х = (3 - х)³, т.е. х³ - 9х² + 26х - 18 = 0

Одним из решений этого уравнения является х = 1. Разделив х³ -- 9х² + 26х - 18 на (х - 1), получим

х³ - 9х² + 26х - 18 =(х - 1)(х² - 8х + 18).

Так как уравнение х² - 8х + 18 = 0 не имеет действительных корней, то единственное решение исходного уравнения — это х = 1.

Ответ:

1

Задание 9.

Ответ:

3

Задание 10.

Ответ:

-1

Задание 11.

Ответ:

Задание 12.

Ответ:

Задание 13.

Решение:

Отметив, что х # 1, преобразуем уравнение к виду

Последнее уравнение равносильно системе

Решив ее, получим х₁ = 1; х₂ = -2. Корень х = 1 посторонний.

Ответ:

-2

Задание 14.

Ответ:

26

Задание 15.

Ответ:

1

Задание 16.

Ответ:

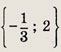
Задание 17.

Ответ:

2

Задание 18.

Ответ:

Задание 19.

Ответ:

{0; 2}

Задание 20.

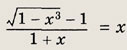
Решение:

Заметив, что х # -1, преобразуем уравнение к виду

Выражение х² + х + 1 > 0 при любых действительных х. Поэтому последнее уравнение равносильно следующему:

1 - х³ = (х² + х + 1)².

Но 1 - х³ = (1 - х)(1 + х + х²), а х² + х + 1 > 0, поэтому приходим к уравнению

1 - х = х² + х + 1, х² + 2х = 0,

откуда х₁ = 0; х₂ = -2.

Ответ:

(-2; 0}

Задание 21.

Ответ:

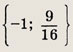
Задание 22.

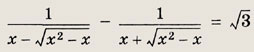
Решение:

Умножим числитель и знаменатель каждой из дробей на сопряженное выражение. Тогда уравнение преобразуется к виду

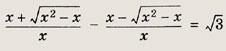
Далее, заметив, что х # 0, получим

Последнее уравнение равносильно системе

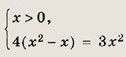
откуда х = 4.

Ответ:

4

 

Решите уравнения (23—32), сводя их к простейшим подходящей заменой:

Задание 23.

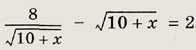
Ответ:

-6

Задание 24.

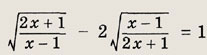
Ответ:

5/2

Задание 25.

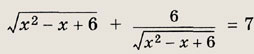
Ответ:

{-5, 6}

Задание 26.

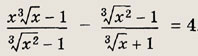
Указание:

Полагая

упростите полученные дроби.

Ответ:

Задание 27.

Решение:

Полагая

сведем уравнение к квадратному относительно у:

4у = 12 - у², т.е. у² + 4у - 12 = 0.

Отсюда у₁ =2; у₂ = -6 (постороннее решение, так как

Поэтому исходное уравнение равносильно уравнению

откуда х₁ + Зх - 6 = 4; х₁ + Зх - 10 = 0. Следовательно, х₁ = -5; х₂ = 2.

Ответ:

{-5; 2}

Задание 28.

Ответ:

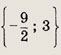
Задание 29.

Ответ:

{-3;6}

Задание 30.

Ответ:

{-7; 2}

Задание 31.

Ответ:

Задание 32.

Ответ:

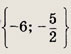
При решении уравнений 33—36 учитывайте области определения входящих в эти уравнения выражений:

Задание 33.

Решение:

Уравнение равносильно системе

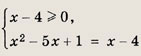
Решив уравнениех² - 6х + 5 = 0, получаем х₁ = 1 (не удовлетворяет первому неравенству), х₂ = 5.

Ответ:

5

Задание 34.

Ответ:

2

Задание 35.

Ответ:

Задание 36.

Ответ:

 

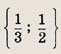
• Если уравнение содержит два или более радикала, то по возможности рекомендуется придерживаться следующих правил:

1) указать область определения данного уравнения;

2) распределить радикалы по обеим частям уравнения так, чтобы обе части стали неотрицательными;

3) только после этого возводить в квадрат правую и левую части уравнения.

Решите следующие уравнения (37-50):

Задание 37.

Решение:

Найдем область определения данного уравнения:

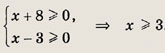
Перенесем

в правую часть равенства, после чего обе части равенства станут неотрицательными. Получаем равносильную систему

Ответ:

28

Задание 38.

Ответ:

{2; 34}

Задание 39.

Ответ:

2

Задание 40.

Ответ:

0

Задание 41.

Решение:

Перепишем уравнение в виде

и найдем область определения данного уравнения:

Возводим в квадрат обе части равенства:

откуда

Последнее уравнение равносильно системе

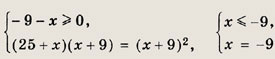
Ответ:

-9

Задание 42.

Ответ:

6

Задание 43.

Ответ:

6

Задание 44.

Ответ:

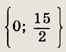
Задание 45.

Решение:

Область определения данного уравнения состоит из всех значений переменной х, удовлетворяющих неравенству

(проверьте!). Переписав уравнение в виде

возведем обе части в квадрат и получим:

Отсюда

Это уравнение равносильно системе

т. е.

Тогда

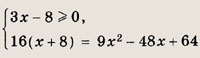
Решив уравнение 9х² - 64х - 64 = 0, получаем

(посторонний корень).

Ответ:

8

Задание 46.

Ответ:

5

Задание 47.

Решение:

Уравнение сводится к простейшему иррациональному уравнению умножением обеих частей равенства на

При этом возможно появление посторонних решений. Поэтому необходимо сразу указать область допустимых значений переменной х. Получаем

При этих х уравнение

равносильно исходному. Решив это уравнение, находим

Значение х = - постороннее.

Ответ:

-3

Задание 48.

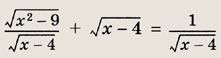
Ответ:

Задание 49.

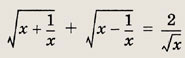
Ответ:

Задание 50.

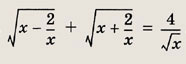
Решение:

Область допустимых значений

При этих х исходное уравнение равносильно следующему:

Возведя в квадрат обе части равенства, приходим к уравнению

Теперь при

снова возведя в квадрат, получаем 16х² = 68. Решение

удовлетворяет неравенству

Ответ:

В уравнениях (51—54) сделайте сначала подходящую замену:

Задание 51.

Решение:

Заменой у = 2х² - Зх уравнение сводится к виду

Решив его, получаем у = -1. Отсюда 2х² - Зх = -1, т. е. 2х² - Зх + 1 = 0.

Ответ:

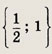
Задание 52.

Ответ:

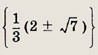
Задание 53.

Решение:

Этот пример значительно труднее предыдущих. Введем новую переменную

Заметим, что у > 0 при всех допустимых х € [2; 4]. Теперь имеем

Отсюда при

получаем

Тогда правая часть исходного уравнения примет вид

а само исходное уравнение примет вид

Раскладывая на множители левую часть последнего равенства, получаем

у²(у² - 4) + 4(у - 2) - У²(у + 2)(у- 2) + 4(у - 2) = (у -2)[у²(у + 2)+ 4] = 0.

Поскольку

единственным решением этого уравнения является значение у = 2. Таким образом, исходное уравнение равносильно уравнению

решив которое, находим х = 3.

Ответ:

3

Задание 54.

Указание:

Положите

Далее см. решение задачи 53 в предыдущем задании.

Ответ:

{1, 5}.

Решите уравнения (55—70):

Задание 55.

Решение:

Запишем уравнение в виде

Мы видим, что уравнение может иметь решение лишь при

Поэтому область допустимых значений, с учетом неравенства

состоит только из тех х, для которых выполнено условие

и точки х = -1. Проверяем, что х = -1 — решение исходного уравнения.
Теперь, сокращая обе части уравнения на

приходим к равносильному при

уравнению:

Решив его, получим х = 1.

Ответ:

{-1; 1}

Задание 56.

Решение:

Перепишем уравнение в виде

Это уравнение может иметь решения лишь при тех ж, для которых справедливо неравенство

Будем проверять его выполнение в дальнейшем. Возведя в квадрат обе части уравнения, получаем

Число х = 0 удовлетворяет выписанному неравенству и, таким образом, является решением исходного уравнения. Решениями оставшегося после сокращения на х уравнения

являются числа х = -1 и х = 1. Оба эти числа удовлетворяют выписанному неравенству.

Ответ:

{-1; 0; 1}

Задание 57.

Ответ:

Задание 58.

Ответ:

Задание 59.

Решение:

При

справедливо неравенство

поскольку функция

монотонно возрастающая. Поэтому удобнее решать уравнение так:

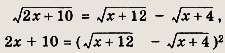
причем последнее уравнение равносильно исходному. Получаем

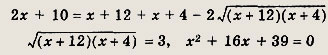
Отсюда х₁ = -3; х₂ = -13 (посторонний корень). Мы привели здесь такое решение потому, что далее, при решении более сложных уравнений и неравенств, нам часто придется отступить от сформулированных перед задачами 37—50 рекомендаций.

Ответ:

-3

Задание 60.

Ответ:

-1

Задание 61.

Ответ:

{-2; 0}

Задание 62.

Решение:

Сделаем замену у = х² + х + 1. Получим уравнение

Решив его, находим у = -4 и у = 1. Уравнение х² + х + 1 = -4 не имеет решений,

а х² + х + 1 = 1, т. е. х² + х = 0, имеет решения x₁ = -1; х₂ - 0.

Ответ:

{-1, 0}

Задание 63.

Решение:

Перепишем уравнение в виде

При

это уравнение равносильно следующему:

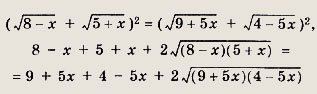
откуда

Снова возводя в квадрат обе части равенства и раскрывая скобки, приходим к уравнению

6х² + 7х + 1 = 0, откуда

Оба решения входят в область допустимых значений.

Ответ:

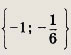
Задание 64.

Ответ:

Задание 65.

Решение:

Сделаем замену

Возводя в квадрат, получаем

Тогда исходное уравнение запишется в виде у = у² - 20, у² - у - 20 = 0, откуда у₁ = 5; у₂ = -4 (постороннее решение, так как

).

Теперь, решив уравнение:

получаем х = 3.

Ответ:

3

Задание 66.

Ответ:

1

Задание 67.

Указание:

Смотри решение задачи 68.

Ответ:

{-6; 1}

Задание 68.

Решение:

Умножим обе части равенства на сопряженное к левой части выражение, т. е. на

Получим

откуда

Решаем это уравнение, сводя его к алгебраической системе (см. далее задачи 71—80). Положим

Тогда величины а и b являются решениями системы

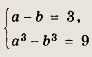
откуда b₁ = -1,b₂ = -2.

Заметим, что значения переменной а можно не находить. Решив два простейших уравнения,

получаем корни х₁ = 4; x₂ = -3.

Ответ:

{-3; 4}

Задание 69.

Решение:

В области определения данного уравнения, т. е. при

- оно равносильно следующему:

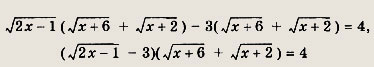
Умножая обе части равенства на разность

получаем

Отметим, что

при всех допустимых значениях переменной х. Следовательно, последнее уравнение равносильно системе

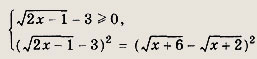
Неравенство дает

а уравнение преобразуется к виду

Решаем это уравнение и получаем x₁ = 3; х₂ = - 7. Решение х = 3 — постороннее, поскольку должно быть

Ответ:

7

Задание 70.

Решение:

Перенося

в правую часть уравнения, получаем

При всех допустимых значениях

правая часть уравнения неотрицательна, так как

при этих значениях х. Но тогда равенство имеет смысл лишь при

При х € [0; 3] исходное уравнение равносильно следующему:

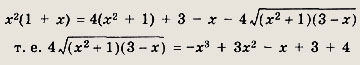
откуда

Теперь легко видеть, что

Корень х = 1 этого уравнения легко находится. Разделив X³ - Зх² + х + 1 на (х - 1), получим квадратное уравнение х² - 2х - 1 = 0.

Решая его, получаем

Второе решение постороннее, так как х € [0; 3].

Ответ:

Решите уравнения (71—80), сведя их к алгебраической системе:

Задание 71.

Решение:

Полагая

приходим к системе

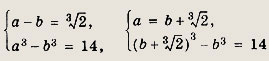
Второе уравнение системы приводится к виду

откуда

Теперь решаем уравнения

Получаем x₁ = -3; х₂ = 3.

Ответ:

{-3; 3)

Задание 72.

Ответ:

9

Задание 73.

Ответ:

0

Задание 74.

Ответ:

2401

Задание 75.

Решение:

Полагая

получаем систему уравнений

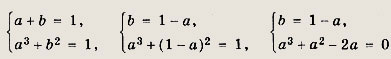
Решив последнее уравнение, находим a₁ = -2; а₂ = 0; а₃ = 1, откуда х₁ =10, х₂ = 2 и х₃ - 1.

Ответ:

1; 2; 10

Задание 76.

Ответ:

{-88; -24; 3}

Задание 77.

Решение:

Полагая

приходим к системе уравнений

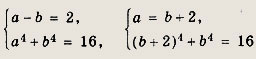
откуда

b⁴ + 8b³ + 24b² + 32b + 16 = 16.

Получаем b(b³ + 8b² + 24b + 32) = 0. Отсюда b = 0, а так как

то уравнение b³ + 8b² + 24b + 32 = 0 решений не имеет.

Итак,

откуда х = 8.

Ответ:

8

Задание 78.

Ответ:

{-79; 1}

Задание 79.

Решение:

Положим

Тогда

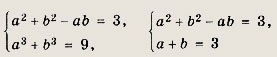
Второе уравнение последней системы получено делением второго уравнения исходной системы на первое уравнение. Подставляя b = 3 - а в первое уравнение, получаем

а² - За + 2 = 0, т.е. а = 1; а = 2.

Решив уравнения

находим х= -2, х = 5.

Ответ:

{-2; 5}

Задание 80.

Решение:

Положим

Тогда а² + b² = 2х + 2, откуда 4 - 2х = 6 - а² - b². Поэтому можно записать систему

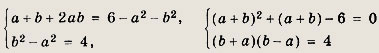
Решив первое уравнение, получаем, что a + b = 2 или a + b = -3. Второе равенство невозможно, поскольку

Таким образом,

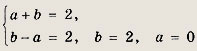
Отсюда находим

Ответ:

1

Примечание:

Сравните решения задач 79, 80, полученные сведением к системе уравнений, с решениями задач того же типа (65—68) другим методом.

Решите уравнения 81—88. В уравнениях 81—84 под каждым радикалом находится полный квадрат некоторого выражения. Выделите его и воспользуйтесь тем, что

Задание 81.

Ответ:

Задание 82.

Решение:

Перепишем уравнение в виде

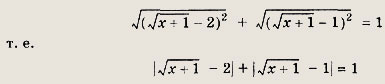
Рассмотрим следующие случаи:

1)

что невозможно;

2)

т. е. в этом случае, при

уравнение выполняется тождественно;

3)

что невозможно.

Ответ:

х € [0; 3]

Задание 83.

Ответ:

(1; 26}

Задание 84.

Ответ:

15

Задание 85.

Решение:

Рассмотрим два случая:

1)

откуда х₁ = -1; х₂ = 23 (посторонний корень);

2)

откуда x₁ = -1; x₂ = 7.

Ответ:

{-1; 7}

Задание 86.

Ответ:

-1

Задание 87.

Ответ:

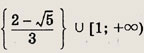
Задание 88.

Решение:

Рассмотрим следующие случаи:

1)

что невозможно;

2)

откуда следует, что

Это также невозможно, поскольку должно быть х > -2.

3)

откуда при

4)

т.е.

3х=3х.

Таким образом, любое число

удовлетворяет уравнению.

Ответ:

Решите следующие системы уравнений (89—101):

Задание 89.

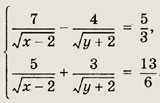
Решение:

Полагая

сведем исходную систему к виду

Тогда

т. е. х = 11, у = 34.

Ответ:

(11; 34)

Задание 90.

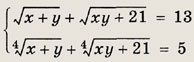
Ответ:

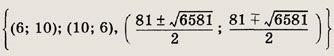
Задание 91.

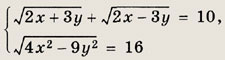
Ответ:

{(17; -10); (17; 10)}

Задание 92.

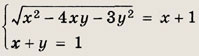
Указание:

Подставьте у = 1 - х в первое уравнение системы.

Ответ:

(2; -1)

Задание 93.

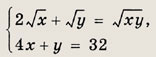
Ответ:

(4; 16)

Задание 94.

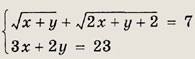
Ответ:

{(5; 4); (-9; 25)}

Задание 95.

Ответ:

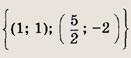
Задание 96.

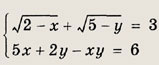
Решение:

Положим

Тогда

Поэтому система перепишется в виде

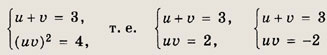
Последняя система не имеет решений, так как должно быть

Получаем u = 1, v = 2 или v = 1, u = 2. Отсюда х = 1; у = 1 или х = -2; у = 4.

Ответ:

{(1; 1); (-2; 4)}

Задание 97.

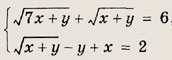
Решение:

Положим

Тогда

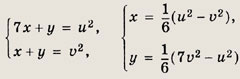
Теперь исходная система примет вид

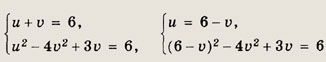
Решив второе уравнение, получаем v = 2 (v = -5 — постороннее решение), а тогда u = 4. Теперь находим переменные (х; у);

Ответ:

(2; 2)

Задание 98.

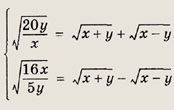
Указание:

Перемножьте уравнения системы.

Ответ:

(5; 4)

Задание 99.

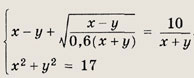
Решение:

Здесь следует рассмотреть два случая.

1) Пусть х + у > 0. Тогда и

Умножая обе части равенства на (х + у), приходим к уравнению

Полагая

получаем

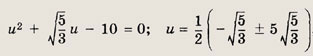
так как

Далее решаем систему

Отсюда

так как из неравенств следует, что

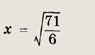
Теперь находим

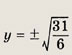
2) Пусть х + у < 0. Тогда и

При этом справедливо равенство

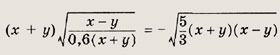
Снова полагая

теперь приходим к системе

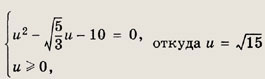
Находим искомые переменные х и у:

откуда х = -4; у = ±1.

Ответ:

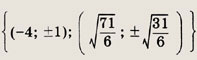
Задание 100.

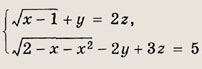
Ответ:

(1; 10; 5)

Задание 101.

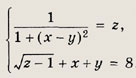
Решение:

Из первого уравнения системы следует, что

а второе определено лишь при

Значит, z = 1. Тогда первое уравнение дает х - у = 0. Следовательно, х = у = 4.

Ответ:

(4; 4; 1)

 

• Простейшее иррациональное неравенство вида

равносильно совокупности следующих двух систем:

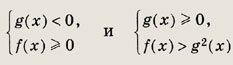
а неравенство вида

равносильно системе неравенств

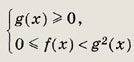
Неравенство

переходит в равносильное после возведения в куб обеих его частей.

Решите следующие неравенства (102—118):

 

Задание 102.

Ответ:

(3; 4]

Задание 103.

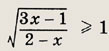
Ответ:

Задание 104.

Ответ:

Задание 105.

Решение:

Неравенство равносильно совокупности двух систем:

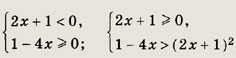
Решив эти системы, получим

Ответ:

Задание 106.

Ответ:

Задание 107.

Ответ:

Задание 108.

Ответ:

Задание 109.

Решение:

Неравенство равносильно системе

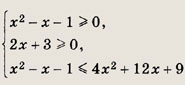
Решив ее, получаем

Ответ:

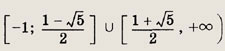
Задание 110.

Ответ:

Задание 111.

Ответ:

Задание 112.

Ответ:

Задание 113.

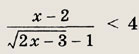
Решение:

Неравенство равносильно совокупности систем:

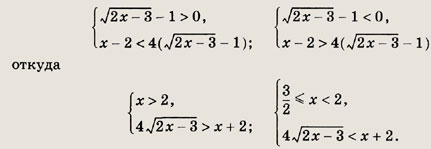
Первая система имеет решение х € (2; 26), а вторая

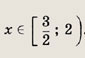
Ответ:

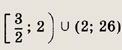
Задание 114.

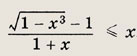
Ответ:

[-2; -1) U (0; 1]

Задание 115.

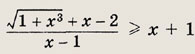
Решение:

Рассмотрим два случая.

1) Пусть х > 1. Тогда неравенство равносильно следующему:

Так как правая часть неравенства строго положительна, то, возводя неравенство в квадрат и сокращая на (х² - х + 1), получим

Учитывая, что х > 1, находим решение х € (1; 2].

2) Пусть теперь х < 1. Тогда

Решив это неравенство, получаем х € [-1; 0].

Ответ:

х € [-1; 0] U (1; 2]

Задание 116.

Ответ:

Задание 117.

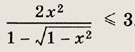
Ответ:

Задание 118.

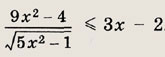
Указание:

Запишите неравенство в виде

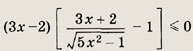
Теперь оно равносильно совокупности

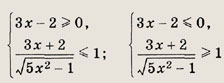
которые легко решаются.

Ответ:

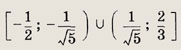
Решите неравенства (119—124), используя тот факт, что соотношения

равносильны:

Задание 119.

Ответ:

Задание 120.

Ответ:

Задание 121.

Ответ:

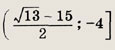
Задание 122.

Ответ:

Задание 123.

Ответ:

[-5; -1]

Задание 124.

Ответ:

[ -1; 1]

Решите неравенства (125—132):

Задание 125.

Решение:

Заметив, что

(это область допустимых значений), возводим обе части неравенства в квадрат. Получаем

откуда

Значит, исходное неравенство равносильно следующей системе:

Решив последнее неравенство, находим:

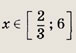
Ответ:

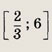
Задание 126.

Ответ:

[-3; 1]

Задание 127.

Ответ:

Задание 128.

Решение:

Найдя область допустимых значений х € [6; 10], перепишем неравенство в виде

Теперь, возводя в квадрат, получаем

Следовательно, исходное неравенство равносильно системе

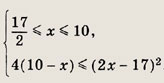
Последнее неравенство преобразуется к виду

Решив его, получаем

Ответ:

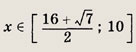
Задание 129.

Ответ:

Задание 130.

Ответ:

Задание 131.

Решение:

Указав область допустимых значений

и переписав неравенство в виде

возводим его обе части в квадрат. Имеем

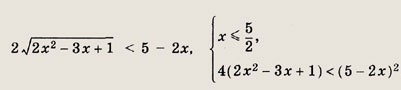
Решив последнюю систему и учитывая, что

получаем

Ответ:

Задание 132.

Ответ:

 

Решите неравенства (133—143), сделав предварительно подходящую замену:

Задание 133.

Ответ:

Задание 134.

Ответ:

[0; 16]

Задание 135.

Ответ:

Задание 136.

Ответ:

Задание 137.

Решение:

Сделав замену х² - 2х - 2 = t и учитывая, что

получим

Теперь при

возводя это неравенство в квадрат, находим t € [0; 1). Таким образом, исходное неравенство равносильно системе квадратичных неравенств

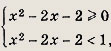
откуда

Ответ:

Задание 138.

Решение:

Сразу запишем область допустимых значений: х € [3; 5]. Сделаем замену, полагая

Тогда

Теперь исходное неравенство перепишется в виде

откуда

Получаем систему неравенств

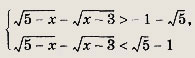
Легко видеть, что ее первое неравенство выполняется при всех допустимых значениях х € [3; 5]. Решаем второе неравенство. Оно приводит к двум системам:

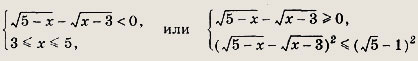
Первая система дает значения х € (4; 5]. Решив вторую, получим

Ответ:

Задание 139.

Ответ:

Задание 140.

Ответ:

Задание 141.

Ответ:

Задание 142.

Ответ:

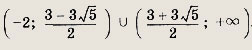
Задание 143.

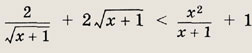
Решение:

Учитывая, что х > -1 и полагая

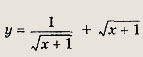
получаем

Поэтому исходное неравенство перепишется в виде

2у < у² - 3, т. е. у² - 2у - 3 > 0.

Отсюда у > 3. Теперь решим неравенство

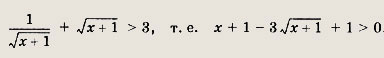
откуда

Возведя в квадрат и учитывая, что х > - 1, получаем решение:

Ответ:

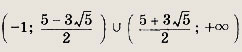
Решите неравенства (144—145), предварительно упростив входящие в неравенства выражения:

Задание 144.

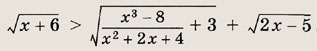
Ответ:

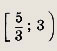
Задание 145.

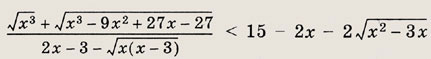
Решение:

Область допустимых значений есть

При этих х получаем

Сокращая первую дробь на

приходим к неравенству

которое решается аналогично неравенствам 138—141 с помощью замены

Имеем

Поэтому исходное неравенство примет вид у² + у - 12 < 0, откуда -4 < у < 3. Решив неравенство

получаем х € [3; 4].

Ответ:

[3; 4]

 

Решите неравенства (146—149), начав с отыскания области допустимых значений:

Задание 146.

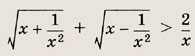
Ответ:

Задание 147.

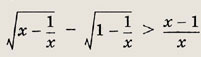
Ответ:

Задание 148.

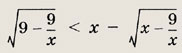
Решение:

Находим область допустимых значений:

Если х € [-3; 0), то правая часть неравенства отрицательна, т. е. при этих значениях х неравенство не выполняется. Рассматриваем далее

В этом случае обе части неравенства неотрицательные. Возведя неравенство в квадрат, получаем

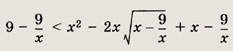
откуда, поделив на х (ведь

), приходим к выражению

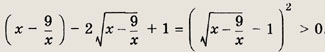
Последнее неравенство выполнено при всех

за исключением корней уравнения

Корень

принадлежит промежутку

и должен быть исключен. Итак,

Заметим, что таким же образом решаются задачи 147 и 149.

Ответ:

Задание 149.

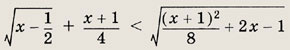
Ответ:

 

Решите следующие неравенства, содержащие знак модуля (150—157):

Задание 150.

Решение:

Учитывая, что

при любом

а

перепишем неравенство в виде

Рассмотрим два случая.

1) Если

то получаем

т. е.

Следовательно, неравенство справедливо при любом х € [0; 9).

б) Если

то получаем

Решив это квадратичное (относительно

неравенство, находим:

Ответ:

Задание 151.

Ответ:

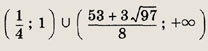
Задание 152.

Ответ:

Задание 153.

Решение:

Имеем

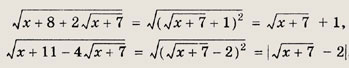
Поэтому неравенство перепишется в виде

Если

то, раскрывая модуль, получаем

что невозможно. Если же

Следовательно,

Ответ:

Задание 154.

Ответ:

Задание 155.

Ответ:

Задание 156.

Ответ:

Задание 157.

Ответ:

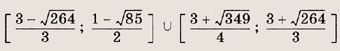
Задание 158.

Проверьте, что каждое решение неравенства

удовлетворяет также неравенству

Решение:

Положим

Тогда следует проверить, что если величины а и b удовлетворяют неравенству а + b > 2, то

т. е. а² + b²> 2. Но

а, следовательно,

а² + b²> 2 при а + b > 2.

 

Решите следующие уравнения и неравенства, содержащие параметры (159—173):

Задание 159.

Ответ:

при

при

Задание 160.

Ответ:

При

при

при

Задание 161.

Решение:

Уравнение равносильно системе

Решив квадратное уравнение, находим

Первый корень при всех допустимых значениях а, т. е. при

удовлетворяет неравенству

Для второго корня получаем

Последнее неравенство выполнено при

Ответ:

при

при

при

Задание 162.

Ответ:

при

при

Задание 163.

Решение:

Уравнение равносильно следующей системе:

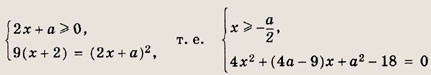
Решив квадратное уравнение, получаем

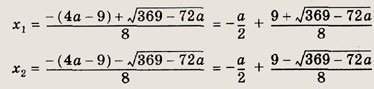
Мы видим, что первый корень xt удовлетворяет нужному неравенству

при всех допустимых значениях а, т. е. при

Для второго корня это неравенство приводит к условию

откуда

Ответ:

при

при

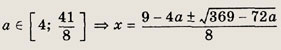
при

Задание 164.

Ответ:

при

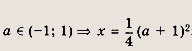
при

Задание 165.

Ответ:

при

при

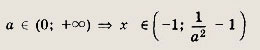
Задание 166.

Решение:

Неравенство равносильно совокупности двух систем:

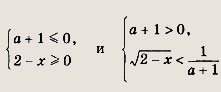
т. е.

при

Ответ:

при

при

Задание 167.

Решение:

Неравенство равносильно следующей системе:

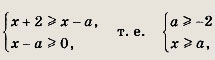
что и дает ответ.

Ответ:

при

при

Задание 168.

Ответ:

при

при

Задание 169.

Ответ:

при

при

Задание 170.

Ответ:

При

при

Задание 171.

Решение:

Неравенство равносильно совокупности систем:

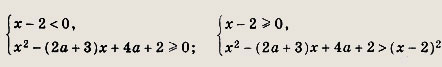
Выполнив преобразования, получаем

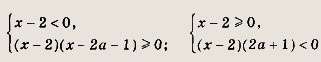
Упрощая системы, приходим к неравенствам

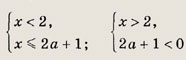
Отсюда если

Если же

то

Ответ:

при

при

Задание 172.

Решение:

Неравенство равносильно совокупности двух систем:

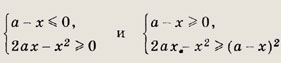
Рассмотрим сначала первую систему. Корни уравнения 2ах - х² = 0 — это числа х = 0 и х = 2а. В зависимости от знака а расположение корней на числовой оси иллюстрируют рис.

Мы видим, что решения первой системы записываются следующим образом:

при

Аналогично решаем вторую систему. Корни уравнения 2х² - 4ах + а² = 0
— числа

В зависимости от знака а теперь расположение корней на числовой оси изображено на рис.

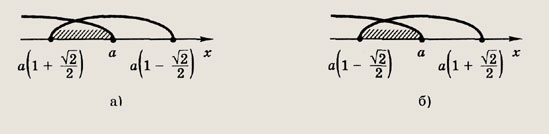
Решение второй системы таково:

Объединяя найденные решения систем, получаем решение исходного неравенства.

Ответ:

Задание 173.

Решение:

Область допустимых значений неравенства есть

Отсюда следует, что

Значение a = 0 приводит к пустому множеству решений. Рассмотрим далее значения а > 0. Возведя в квадрат, получаем

откуда при а € (0; 2] => х € [-а; а]. Если

то, снова возведя неравенство в квадрат, имеем

4х²< а³(4 - а),

откуда при

а при

Объединяя полученные решения, записываем ответ.

Ответ:

при

при а € (0;2) => х € [-a;a]
при

Задание 174.

Найдите все а, при которых решения уравнения

существуют и принадлежат отрезку [2; 27].

Ответ:

а € [1; 5]

Задание 175.

Найдите все а, при которых решения уравнения

существуют и принадлежат отрезку [2; 17].

Решение:

Преобразовав уравнение к виду

и введя новую переменную

переформулируем условие задачи следующим образом: найти такие а, при которых решения уравнения

|t - 2| + |t - 3| = а существуют и принадлежат отрезку [1; 4]. Проиллюстрируем решение на рисунке, построив график функции у = |t - 2| +|t - 3|.

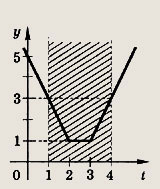
Мы видим, что решения уравнения существуют при

но принадлежат отрезку [1; 4] лишь при а € [1; 3].

Ответ:

а € [1; 3].

Задание 176.

При каких а решения неравенства

образуют на числовой оси прямой отрезок длины 2|а|?

Ответ:

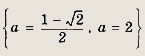
Задание 177.

При каких а решения неравенства

образуют на числовой оси прямой отрезок длины 3|а|?

Решение:

Данное неравенство равносильно совокупности систем:

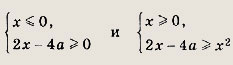
Первая система имеет следующее решение: при

при

а вторая — при

при

при

Объединяя решения систем, получаем: при

решением системы является отрезок

Его длина равна 3|а| в том случае, когда а (а < 0) удовлетворяет уравнению

Если же

то решения данного неравенства заполняют отрезок

Его длина равна

в том случае, если

откуда

Ответ:

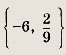
Задание 178.

При каких а множество решений неравенства

содержит все целые отрицательные числа?

Указание:

Все целые отрицательные числа

являются решениями этого неравенства при выполнении условия

т. е. при

так как

Остается установить, при каких а числа х = -1 их = -2 также являются решениями этого неравенства.

Ответ:

Решите следующие уравнения (179—182), сведя их к системе:

Задание 179.

Ответ:

При

при

при

при а

Задание 180.

Ответ:

При

при

при

Задание 181.

Решение:

Очевидно, что

Если а = 0, то х = 0 — единственное решение уравнения. Рассматриваем далее значения а > 0. Полагая

приходим к системе

Раскладывая последнее уравнение на множители и учитывая, что

имеем

Решив это уравнение, получим

Равенство

не выполняется ни при каких действительных значениях а. Рассмотрим равенство

Оно справедливо при

При этом

Ответ:

при

при

Задание 182.

Решение:

Если а = 0, то решением уравнения является любое. число

Если же а # 0, то, умножая обе части равенства на

и сокращая на 2а, приходим к уравнению

Полагая

получаем систему

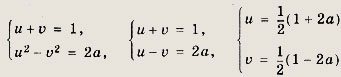
Так как

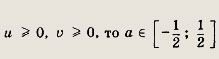
При этих а находим

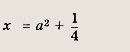
Ответ:

при

при

при

Ответ:

• При решении многих задач, содержащих параметры, часто решающим оказывается умение построить графики функций, входящих в уравнение или неравенство данной задачи. Графиком функции

является часть параболы х - у², расположенная в полуплоскости

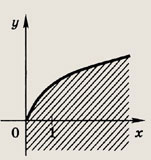
На рис. штриховкой отмечено также множество всех точек М(х; у), координаты которых удовлетворяют
неравенству

В задачах (183—193) постройте графики указанных функций (или уравнений). Отметьте штриховкой области, определяемые указанными неравенствами:

Задание 183.

Ответ:

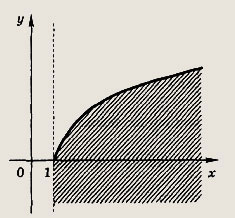
Задание 184.

Ответ:

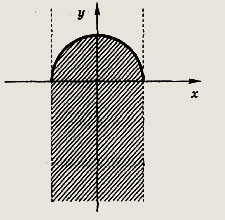
Задание 185.

Ответ:

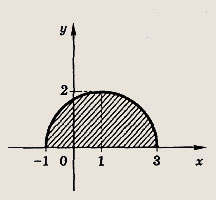
Задание 186.

Ответ:

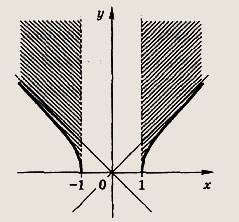
(часть гиперболы х² - у² = 1 в полуплоскости у > 0)

Задание 187.

Решение:

Нужно заштриховать область, координаты точек которой удовлетворяют системе неравенств

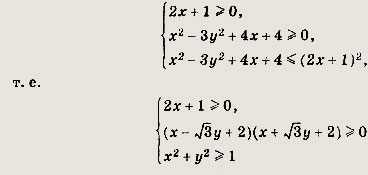
Эта область изображена на рис.

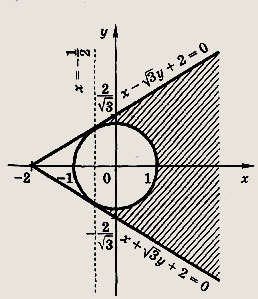
Прямые

касаются окружности

Задание 188.

Решение:

Нужно заштриховать множество точек, координаты которых удовлетворяют совокупности неравенств

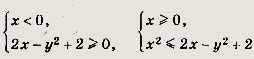
Эта область изображена на рис.

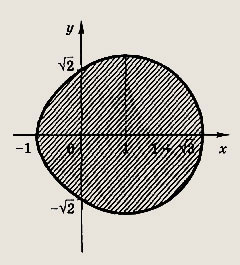
При х < 0 она ограничена параболой

— окружностью (х - 1)² + у² = 3.

Задание 189.

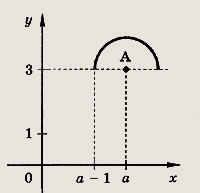
Что происходит с графиком функции при изменении параметра а?

Указание:

Это — верхняя половина окружности

(х² - а)² + (у - З)² = 1 с центром А(а; 3). При увеличении а полуокружность целиком смещается вправо.

Ответ:

Задание 190.

Ответ:

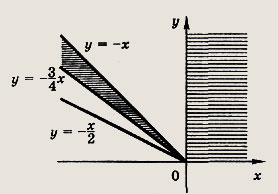
где заштриховано множество точек:

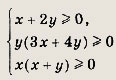
Задание 191.

Ответ:

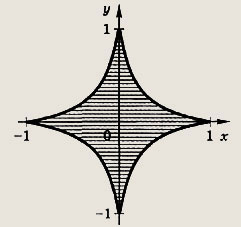
(область ограничена астроидой J\x\ + J\y] =1)

Задание 192.

Указание:

Возведя равенство в квадрат, приведите его к виду

Постройте этот график (гиперболу), складывая графики функций

Ответ:

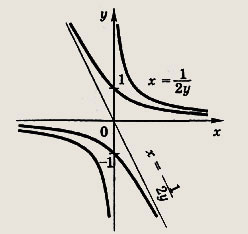
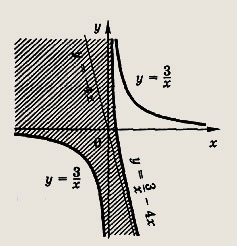
Задание 193.

Решение:

Неравенство равносильно совокупности систем

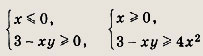
т. е. в искомую область входят точки оси Оу и точки, удовлетворяющие системам

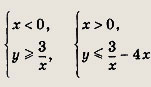
Эта область изображена на рис.

 

 

Решите следующие задачи (194—203), используя графики:

Задание 194.

Найдите значение параметра а, при которых уравнение

имеет ровно два решения.

Ответ:

Задание 195.

Найдите все а, при которых уравнение

имеет единственное решение.

Ответ:

Задание 196.

Найдите все а, при которых уравнение

имеет единственное решение.

Решение:

Запишем уравнение в виде

и построим графики функций

Первый график — это верхняя половина окружности у² +(х + З)² = 1. Графики прямых у = (1 - а) - х пересекают ось ординат в точках А (0; 1 - а). Мы видим, что уравнение имеет единственное решение при таких а, что

Кроме того, единственное решение получается и в том случае, если прямая у = (1 - а) - х — касательная к верхней половине окружности у² + (х + З)² = 1. Вычислив нужное значение а, получаем

Ответ:

Задание 197.

Найдите все а, при которых уравнение

имеет единственное решение.

Указание:

Постройте графики функций

Ответ:

Задание 198.

При каких а уравнение

имеет единственное решение?

Указание:

Постройте графики функций

и проследите, что происходит с ними при изменении значения параметра а (см. задачу 189).

Ответ:

a € [2; 3) U (3; 4]

Задание 199.

При каких а система неравенств

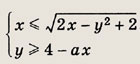
имеет решения?

Указание:

Постройте область, координаты точек которой удовлетворяют неравенству

(см. задачу 188). Далее проследите, при каких а полуплоскость

пересекается с указанной областью.

Ответ:

Задание 200.

Найдите все значения а, при которых система неравенств

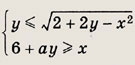
имеет решения.

Ответ:

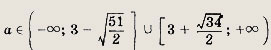
Задание 201.

Найдите все значения а, при каждом из которых система

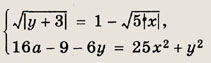
имеет ровно четыре решения.

Решение:

Сделав замену переменных у + 3 = u; 5х = V, сведем задачу к следующей: найдем, при каких а система

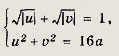
имеет ровно четыре решения. Строим в плоскости (u; v) графики

(астроида; см задачу 191) и u² + v² = 16a (окружность радиуса

) при a > 0. Эти кривые изображены на рис.

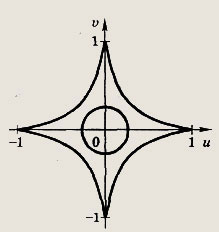
В силу их симметрии уравнение будет иметь четыре решения либо если окружность касается астроиды в этом случае, как легко видеть,

),

либо окружность проходит через точку А(1; 0)

Ответ:

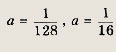
Задание 202.

Найдите все значения а, при которых всякая пара чисел (х; а), удовлетворяющая неравенству

удовлетворяет также неравенству

Решение:

Отметим штриховкой

в плоскости (х; а) области, где выполняются неравенства:

(горизонтальная штриховка),

(вертикальная штриховка).

Мы видим, что решения первого неравенства включают все решения второго неравенства лишь при а < а₀. Для подсчета а₀ найдем Х₀ —- корень уравнения

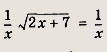
Получаем х₀ = -3, а тогда

Замечание.

В отличие от всех предшествующих задач, где мы строили для обоснования графики стандартных функций (прямые, параболы, окружности и гиперболы), здесь мы опирались на построение графика функции

Поэтому приведенное решение можно признать недостаточно строгим (но полезным). Приведем другое решение этой задачи, просто решив неравенство

Сразу отметим, что при а > 0 решения этого неравенства не могут включать бесконечный интервал

Поэтому достаточно рассмотреть случай а < О. Неравенство

равносильно совокупности систем:

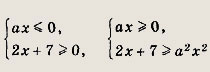
При a < 0 первая система дает

а вторая система — решение

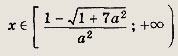
Для выполнения условия задачи необходимо, чтобы

Решив это неравенство при а < 0, получаем

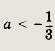
Ответ:

Задание 203.

Найдите все отрицательные значения а, при которых числа х, не превосходящие по модулю числа

удовлетворяют неравенству

Ответ:

а € [-1; 0)

 

Решите системы неравенств (204—205):

Задание 204.

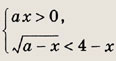
Решение:

Исходная система равносильна выполнению следующих условий:

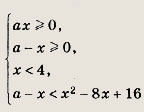
Заштрихуем в плоскости (х; а) точки, координаты которых удовлетворяют этим условиям.

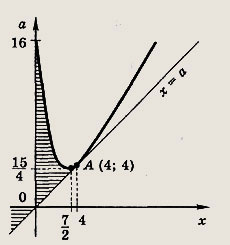
Прямая х = а касается параболы а = х² - 7х + 16 в точке А(4; 4). Решив уравнение х² - 7х + 16 - а = 0, получим выражения

которые задают правую и левую половины параболы. Теперь можно записать решения неравенства.

Ответ:

при

при

при

при

при

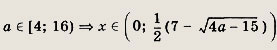
Задание 205.

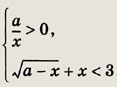
Ответ:

При

при

при

при

при

Задание 206.

При каких а неравенство

не имеет решений?

Решение:

Запишем неравенство в виде

и построим графики левой и правой частей этого неравенства. Рассмотрим два случая:

Если

то решений не будет при всех а > а₀

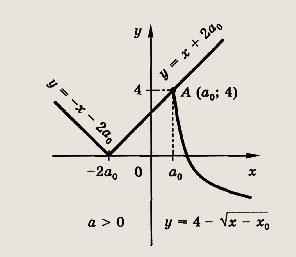
Число а₀ находим из условия, что точка А(а₀; 4) лежит на прямой у = х + 2а. Отсюда

Случай а < 0 несколько сложнее. Здесь нужное неравенство не будет иметь решений, если а < min(a₁ a₂), где число а₁ находим из условия, что точка A(a₁; 4) лежит на прямой у = -х - 2a₁; а число a₂ из условия, что

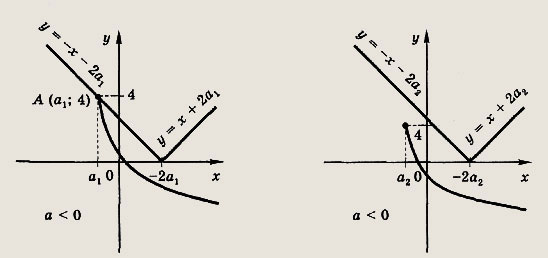
Получаем

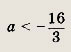
Ответ:

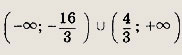
Задание 207.

При каких значениях параметра а система уравнений

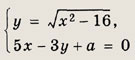
имеет единственное решение?

Указание:

См. задачу 186, где была построена подобная гипербола.

Ответ:

Задание 208.

При каких а система

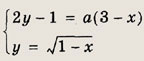
имеет решения?

Решение:

Строим графики:

— верхнюю часть параболы;

-прямые, проходящие через точку

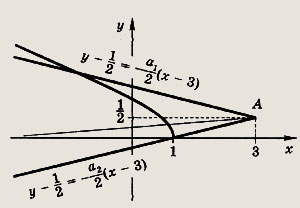
Найдем среди этих прямых касательную к верхней части параболы и прямую, проходящую через точку (1; 0). Подсчеты дают для этих прямых значения

При всех

прямые пересекают эту часть параболы. Система имеет решения.

Ответ:

Задание 209.

Найдите наименьшее значение выражения

если х + 2у = 2.

Ответ:

Задание 210.

Найдите все пары чисел (х; у), удовлетворяющие уравнению

х² + у² - 6x + 4у + 11 = 0,

при которых значение выражения

наибольшее.

Ответ:

(4; -1)