Степени и корни.
Тождественные преобразования числовых и алгебраических выражений
• Основой для тождественных преобразований числовых и алгебраических выражений
служат формулы сокращенного умножения:
(а + b)2 = а2 + 2аb + b2;
(а - b)2 = а2 -2аb + b2;
(а + b)3 =a3 + 3a2b + 3ab2 + b3;
(а - b)3 = а3 - За2b + Заb2 - b3;
а2 - b22 = (а - b) (а + b);
а3 - b3 = (а - b)(а2 + аb + b2);
а3 + b3 = (а + b)(а2 - ab + b2).
Принято считать, что все тождественные преобразования выполняются в области определения выражений, входящих в рассматриваемую задачу. При этом в ответе сама эта область, как правило, не указывается.
Упростите следующие выражения (1—26):
Задание 1.
![]()
Ответ:
0
Задание 2.
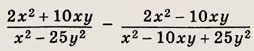
Ответ:
0
Задание 3.
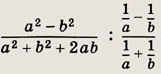
Ответ:
-1
Задание 4.
![]()
Ответ:
а - b
Задание 5.
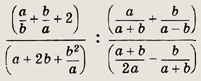
Ответ:
![]()
Задание 6.
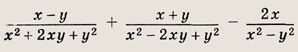
Ответ:
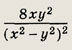
Задание 7.
![]()
Ответ:
![]()
Задание 8.
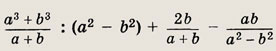
Ответ:
1
Задание 9.
![]()
Ответ:
![]()
Задание 10.
![]()
Ответ:
0
Задание 11.
![]()
Ответ:
1
Задание 12.
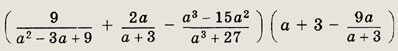
Ответ:
а + 3
Задание 13.
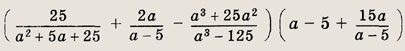
Решение:
Учитывая, что а3 - 125 = (а - 5)(а2 + 5а + 25), и приводя дроби к общему знаменателю, получаем
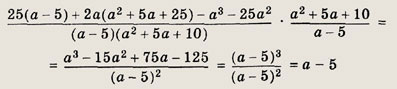
Ответ:
а - 5
Задание 14.
![]()
Ответ:
![]()
Задание 15.
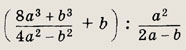
Ответ:
4
Задание 16.
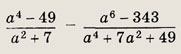
Ответ:
0
Задание 17.
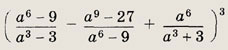
Ответ:
а9
Задание 18.
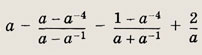
Ответ:
![]()
Задание 19.
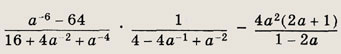
Ответ:
(2а + 1)2
Задание 20.
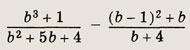
Ответ:
0
Задание 21.
![]()
Ответ:
0
Задание 22.
![]()
Решение:
Заметим, что а3 + 27 = (а + 3)(а2 - За + 9), а2 + 7а = 12 = (а + 3)(а + 4). Теперь получаем
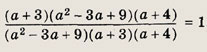
Ответ:
1
Задание 23.
![]()
Ответ:
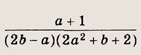
Задание 24.
![]()
Ответ:
![]()
Задание 25.
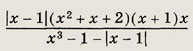
Решение:
1) Если х > 1, то |x - 1| = х - 1. Тогда
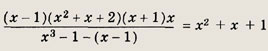
2) Если х < 1, то |х - 1| = 1 - х, откуда
![]()
Ответ:
при х > -1 => х2 + х + 1; при х < 1 => -х2 - х.
Задание 26.
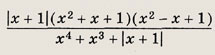
Ответ:
При
![]()
при
![]()
Решите уравнения (27—34):
Задание 27.
(х - 1)3 = x(x + 2)2 - 9
Ответ:
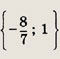
Задание 28.
(x + 2)3 =5 x(x - 1)2 + 62
Ответ:
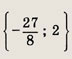
Задание 29.
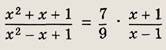
Ответ:
2
Задание 30.
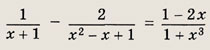
Указание:
х = -1 не входит в область допустимых значений.
Ответ:
2.
Задание 31.
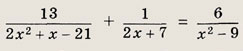
Решение:
Запишем уравнение в виде
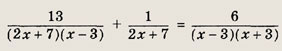
Приведем дробь к общему знаменателю и получим квадратное уравнение х2
+ х -12=0. Его корни X1 = -4, Х2 = 3. Корень х = 3 не
входит в область допустимых значений и его нужно отбросить.
Ответ:
{-4}
Задание 32.
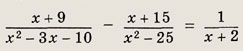
Ответ:
{-8}
Задание 33.
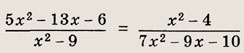
Ответ:
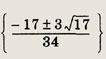
Задание 34.
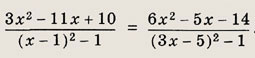
Ответ:
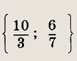
Найдите числа а, b, с, d такие, что выполняются заданные равенства (35—38):
Задание 35.
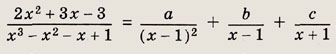
Ответ:
a = 1; b = 3; с = -1
Задание 36.
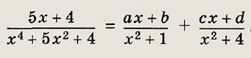
Ответ:
![]()
Задание 37.
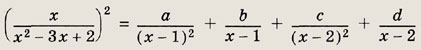
Решение:
Отметим, что (х2 - Зх + 2)2 = (х - 1)2(х - 2)2. Заданное равенство есть равенство двух дробей, из которых одна представлена в виде суммы простейших дробей. Имеем
![]()
Приравняем числители этих дробей:
а(х - 2)2 + b(х - 1)(х - 2)2 + с(х - 1)2 + d(x - 2)(х - 1)2 = х2.
Полагая в этом равенстве х = 1, находим а = 1, а, полагая х = 2, получим с = 4. При а = 1 и с = 4 перепишем равенство в виде
(х - 2)2 + 4(х - 1)2 - х2 = (1 - х)(2 - х)2b + (2 - х)(1 - x)2d.
Теперь положим в этом равенстве х = 0 и получим 4b + 2d = 8, т. е. 2b + d = 4; далее, при х = -1 имеем 18b + 12d = 24, т. е. Зb + 2d = 4. Решив полученную систему, найдем b = 4; d = -4.
Ответ:
а = 1; b = 4; с = 4; d = -4
Задание 38.
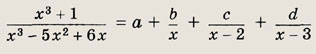
Решение:
Поделив х3 + 1 на х3 - 5х + 6х с остатком, имеем
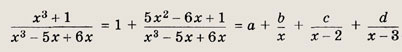
откуда а = 1, а для вычисления коэффициентов b, с и d получаем равенство
b(х - 2)(х - 3) + сх(х - 3) + dx(x - 2) = 5х2 - 6х + 1.
Взяв х = 0, находим 6b = 1, т. е
![]()
Взяв х = 2, находим -2с = 9, откуда
![]()
Наконец, при х = 3, имеем 3d = 28, откуда
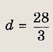
Ответ:
![]()
Постройте графики функций (39, 40):
Задание 39.
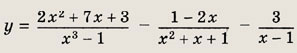
Указание:
Упростив правую часть равенства, получим
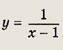
Ответ:
График — гипербола.
Задание 40.
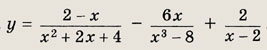
Указание:
Упростив правую часть равенства, получим
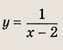
Ответ:
График — гипербола.
• Напомним, что символом
![]()
обозначается арифметический корень из неотрицательного числа а, т. е. неотрицательное число b, такое, что b2 - а (соответственно b2n = а). Символ
![]()
обозначает любое число b, такое, что b2n + 1 - а. Справедливы равенства:
![]()
Далее, если
![]()
— рациональное число, а число а > 0, то по определению
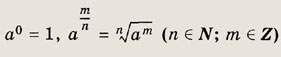
Наконец, напомним правила действия со степенями. Если числа а, b > О, a r1
и г2 — любые рациональные числа, то:
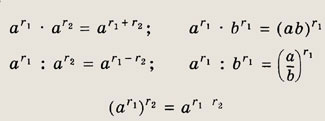
Отметим, что для многих показателей r степень аr определена на более
широком множестве. Так, выражение
![]()
определено при всех
![]()
а
![]()
— вообще для всех а € R.
Упростите выражения (41—63):
Задание 41.
-(0,5)2 : (0,5)3 - 271/3 + 44 • 4-2 - (0,2)0
Ответ:
10
Задание 42.
![]()
Ответ:
![]()
Задание 43.
![]()
Ответ:
8
Задание 44.
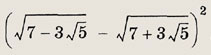
Ответ:
10
Задание 45.
![]()
Ответ:
-3
Задание 46.
![]()
Ответ:
![]()
Задание 47.
![]()
Ответ:
а-2
Задание 48.
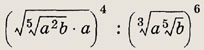
Ответ:
а4/5
Задание 49.
![]()
Ответ:
2аb-1
Задание 50.
![]()
Ответ:
![]()
Задание 51.
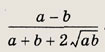
Ответ:
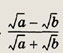
Задание 52.
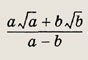
Ответ:
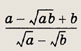
Задание 53.
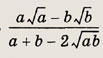
Ответ:
![]()
Задание 54.
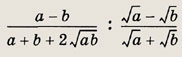
Ответ:
1
Задание 55.
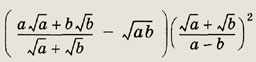
Ответ:
1
Задание 56.
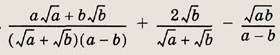
Ответ:
1
Задание 57.
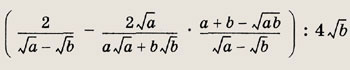
Ответ:
![]()
Задание 58.
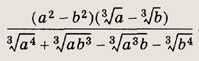
Ответ:
а + b
Задание 59.
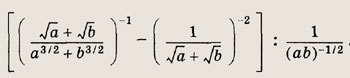
Ответ:
-3
Задание 60.
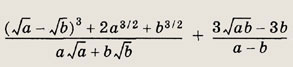
Ответ:
3
Задание 61.
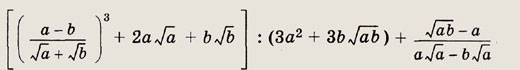
Ответ:
0
Задание 62 .
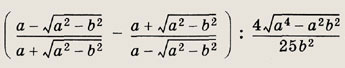
Ответ:
-25
Задание 63.
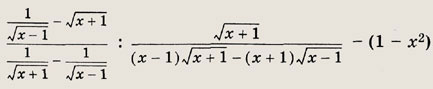
Ответ:
![]()
Упростив правые части равенств, решите уравнения (64—67):
Задание 64.
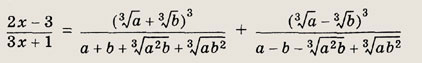
Ответ:
![]()
Задание 65.
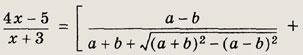
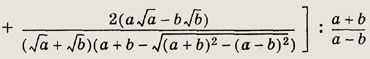
Ответ:
14
Задание 66.
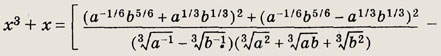
![]()
Решение:
Преобразуя правую часть равенства, имеем:
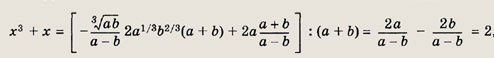
т. е. х3 + х - 2 = - 0. Далее, раскладывая левую часть последнего
уравнения на множители, получаем
х3 + х - 2 = (х - 1)(х2 + х + 2) = 0, откуда х = 1.
Ответ:
1
Задание 67.
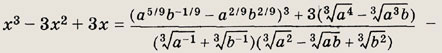
![]()
Ответ:
1
Упростите следующие числовые и алгебраические выражения (68—79):
Задание 68.
![]()
Ответ:
![]()
Задание 69.
![]()
Указание:
Найдите числа а и b такие, что a2 +b2 = 18,
![]()
Тогда под корнем окажется выражение (а + b)2.
Ответ:
![]()
Задание 70.
![]()
Ответ:
2
Задание 71.
![]()
Указание:
![]()
Ответ:
-2
Задание 72.
![]()
Решение:
Положим
![]()
Тогда, используя формулу (а + b)3 = а3 + b3 + Заb(а + b), получим
![]()
Таким образом, х3 = 4 - Зх, т. е. х3 + Зх - 4 = 0. Раскладывая
левую часть этого уравнения на множители, имеем (х - 1)(х2 + х +
4) = 0, т. е. х = 1.
Ответ:
1
Задание 73.
![]()
Ответ:
4
Задание 74.
![]()
Ответ:
3
Задание 75.
![]()
Ответ:
![]()
Задание 76.
![]()
Решение:
Так как
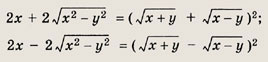
то
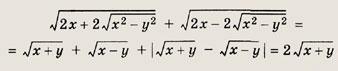
Мы воспользовались тем, что
![]()
Ответ:
![]()
Задание 77.
![]()
Указание:
После извлечения квадратных корней выражение примет вид
![]()
Ответ:
![]()
если
![]()
1, если
![]()
если
![]()
Задание 78.
![]()
Решение:
Так как
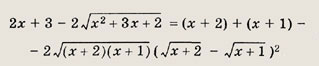
то при
![]()
получаем
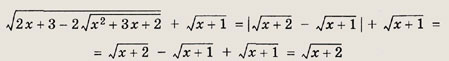
Мы воспользовались тем, что при
![]()
Ответ:
![]()
Задание 79.
![]()
Указание:
![]()
Ответ:
![]()
при
![]()
![]()
при
![]()
Постройте графики функций (80—83):
Задание 80.
![]()
Ответ:
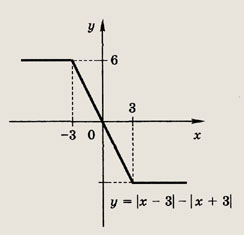
Задание 81.
![]()
Ответ:
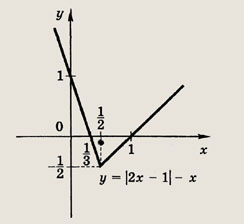
Задание 82.
![]()
Ответ:
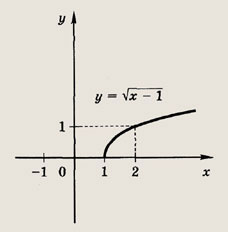
Задание 83.
![]()
Ответ:
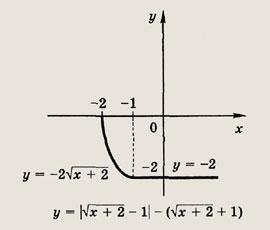
Разложите на множители многочлены (84—89):
Задание 84.
х4+ х2 + 1
Указание:
х4 + х2 + 1 = х4 + 2х2 + 1 -- х2 = (х2 + 1)2 - х2.
Ответ:
(х2 - х + 1)(х2 + х + 1).
Задание 85.
х8 + х4 + 1
Решение:
Имеем
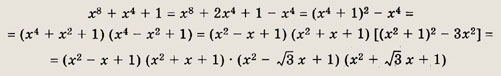
Квадратные трехчлены в скобках далее на множители не раскладываются (у всех
этих трехчленов отрицательные дискриминанты).
Ответ:
![]()
Задание 86.
9х2 - 6х - у2 + 2у
Ответ:
(Зх - у)(3х + у - 2)
Задание 87.
х2 - 2х - 4у2 + 4yz + 1 - z2
Ответ:
(х + 2у + z - 1)(х - 2у - z - 1)
Задание 88.
х4 + у4
Ответ:
![]()
Задание 89.
х4 + у4 + х2 у2
Решение:
Получаем
х4 + у4 + Х2у2 = х4 + у4 + 2х2у2 - х2у2 = (х2 + у2)2 - (ху)2 = (х2 + у2 + ху) (х2 + у2 - ху).
Ответ:
(х2 + у2 + ху) (х2 + у2 - ху).
Задание 90.
Найдите все пары чисел (х; у), удовлетворяющие уравнению:
а) 2х2 + 5у2 + 2ху - 8х + 2у + 10 = 0
б) 10x2 - 10ху + 5у2 + 2х - 8у + 5 = 0
Решение а).
Замечаем, что 2х2 + 5у2 + 2ху = (х + 2у)2 + (х - у)2.
Теперь подберем числа а и b так, чтобы
(х + 2у + а)2 + (х - у + b)2 = 2х2 + 5у2 + 2ху - 8х + 2у + 10.
Приравнивая коэффициенты при подобных членах, имеем
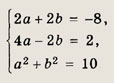
откуда а = -1; b = -3.
Таким образом, исходное уравнение равносильно уравнению
(х + 2у - 1)2 + (х - у - З)2 = 0, т. е.
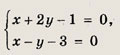
Решив систему, получаем
![]()
Отметим, что это решение
можно также получить, решив уравнение относительно одной из
переменных, например «х».
Указание к b:
10х2 - 10ху +
5у2 = (3х - 2у)2 + (х + у)2.
Далее см. решение задачи 90 а).
Ответ:
а)
![]()
b)
![]()
Задание 91.
Найдите все целочисленные решения уравнений:
а) х3 - 6х2 - ху + 13х + Зу + 7 = 0
б) 2х3 - 9х2 - ху - 6х + 5у + 12 = 0
Решение b):
Запишем уравнение в виде у(х - 5) = 2х3 - 9х2 - 6х + 12, откуда, поделив его правую часть на (х - 5) с остатком, получим
![]()
Мы ищем целочисленные решения уравнения. Значит, число (х - 5) должно быть целым
делителем числа 7. Отсюда следует:
х - 5 = 1=>х = 6, у
=84;
х - 5 = -1 => х = 4, у = 28;
x - 5 = 7=>x = 12, у= 300;
х - 5 = -7 => х = -2, у = 4.
Ответ:
а) {(4; 27); (2; -17); (22; 423); (-16; 307)}
б) {(-2; 4), (4; 28), (6; 84), (12; 30)}
Задание 92.
Проверьте, что число
![]()
удовлетворяет уравнению х3 + 2bх - 2а = 0.
Указание:
Найдите х3, используя формулу (u - v)3 = u3 - u3 -- 3uv(u - v).
Задание 93.
Проверьте, что если
![]()
то х2/3 + у2/3 = а2/3 .
Решение:
Имеем
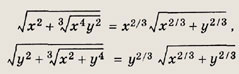
и, следовательно,
![]()
Отсюда и получаем нужное равенство.
