Варианты проверочных работ
Вариант 1
Задание 1.
Найдите длину вектора
![]()
![]()
Задание 2.
Даны точки А(-1; 2; 2) и B(3; 1; 2). Найдите расстояние от начала координат до середины отрезка АВ.
Задание 3.
При каком значении m векторы
a = {1; m; -2} и
![]()
взаимно перпендикулярны?
Задание 4.
Даны вершины треугольника А(-1; 1), В(-5; 4) и С(7; 2). Найдите скалярное произведение векторов
![]()
и
![]()
и площадь треугольника ABC.
Задание 5.
Составьте уравнение окружности, описанной около треугольника, образованного прямой Зх - y + 6 = 0 и осями координат.
Задание 6.
Составьте уравнение сферы, проходящей через точку А(1; -1; 4) и касающейся координатных плоскостей.
Задание 7.
В параллелограмме ABCD (АВ || CD) BM -- высота,
![]()
Разложите зектор ВМ по векторам
![]()
Задание 8.
Начало А(x0 ; y0 ) вектора
![]()
лежит на графике функции
![]()
где х0 — точка минимума этой функции, а конец В — на графике функции
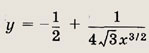
Найдите координаты вектора
![]()
если его длина наименьшая.
Вариант 2
Задание 1.
Какой угол образуют единичные векторы
![]()
если известно, что векторы
![]()
перпендикулярны?
Задание 2.
Найдите длины сторон и величины углов треугольника с вершинами А(2; -3; 0), B(2; -1; 1) и С(0; 1; 4).
Задание 3.
Разложите вектор а = {0; 3; -1} по векторам
![]()
Задание 4.
Медианы боковых сторон равнобедренного треугольника пересекаются под углом 60°. Найдите угол при вершине треугольника.
Задание 5.
Около квадрата со стороной а описана окружность. Найдите сумму квадратов расстояний от точки этой окружности до вершин квадрата.
Ответ:
Задание 6.
В декартовой прямоугольной системе координат Оху к кривой
![]()
в ее точке А(х0; у0), где х0 = 1, проведена касательная. Она пересекает ось абсцисс в точке В, а ось ординат — в точке С. Запишите разложение вектора
![]()
по векторам
![]()
Задание 7.
Составьте уравнение окружности, вписанной в треугольник, стороны которого лежат на прямых х = 0, у = 0 и Зх + 4у - 12 = 0.
Задание 8.
Дан куб ABCDA1B1C1D1 с ребром АА1 = а. Точка Е1 -середина ребра В1С1. Найдите радиус сферы, проходящей через точки А1, Е1, С1 и С.
Вариант 3
Задание 1.
Векторы
![]()
образуют угол
![]()
![]()
Найдите угол между векторами
![]()
Задание 2.
Вычислите координаты вершин С равнобедренного прямоугольного треугольника ABC, если А(0; 8), В(6; 0) и < ABC = 90°.
Задание 3.
Даны векторы
![]()
Найдите разложение вектора
![]()
b и с, если известно, что
![]()
Задание 4.
Найдите расстояние от середины отрезка АВ до плоскости 2х - у + z = 0, если А(-1; 3; 2), B(3; 1; 2).
Задание 5.
В треугольнике ABC |АВ| = с, |ВС| = а, |АС| = b, причем а2 + b2 = 5с2. Найдите угол между медианами треугольника, проведенными к сторонам АС и ВС.
Задание 6.
В куб вписана сфера. Найдите сумму квадратов расстояний от точки сферы до вершин этого куба, если ребро куба равно а.
Задание 7.
Дан куб ABCDA1B1C1D1 (AA1 || BB1 || CC1 || DD1) c ребром а, Р — середина ребра C1В1. Внутри куба находится поверхность S, состоящая из точек М, для которых MD1 : МР =4 :3. Найдите площадь поверхности S.
Задание 8.
Запишите уравнение сферы, проходящей через начало координат и кривую, заданную уравнениями