Варианты проверочных работ
Вариант 1
Решите уравнения:
Задание 1.
|х + 2| = 2(3 - х)
Задание 2.
6х + х|х + 3| + 8 = 0
Задание 3.
|х - 2| = а - х
На координатной плоскости отметьте штриховкой множество точек, координаты которых удовлетворяют неравенствам 4, 5:
Задание 4.
![]()
Задание 5.
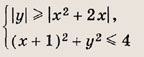
Задание 6.
При каких значениях а уравнение |х2 + 2ах| = 1 имеет три решения?
Задание 7.
Разность цифр двузначного числа по модулю не превосходит 3, а сумма цифр равна 9. Найдите это число.
Задание 8.
Найдите площадь фигуры, заданной на координатной плоскости неравенством
![]()
Вариант 2
Решите уравнения:
Задание 1.
|2х - 3| - |2х + 4| = 3
Задание 2.
|х + 3| = -х2 - 4х - 3
Задание 3.
||х +1| + х| = а
На координатной плоскости отметьте штриховкой множество точек, координаты которых удовлетворяют неравенствам 4, 5:
Задание 4.
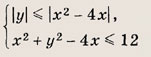
Задание 5.
![]()
Найдите площадь полученной фигуры.
Задание 6.
При каких а все решения уравнения 2|х - а |+ а + + х - 4 = 0 принадлежат отрезку [0; 4]?
Задание 7.
Найдите наибольшее значение функции у = |х - а| на отрезке [1; 3].
Задание 8.
При каких а система уравнений
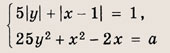
имеет ровно четыре решения?
Вариант 3
Решите уравнения:
Задание 1.
|2х - х|х + 1|| - х2 - 2
Задание 2.
2|х| + |х - 1| = а
Задание 3.
|х2 - 6х + 5| = 2ах
Задание 4.
Постройте график уравнения у2 = |4 - х2|
Задание 5.
На координатной плоскости отметьте штриховкой множество точек, координаты которых удовлетворяют неравенству
![]()
Задание 6.
При каких а уравнение х2 - 2а|х| + а2 - 1 = 0
имеет решения, причем все эти решения принадлежат отрезку [-3; 4]?
Задание 7.
Найдите пары чисел а и b, при которых уравнение |х2 - 2ах| = b2 - 8b имеет ровно три различных решения, причем сумма этих решений равна 9.
Задание 8.
Найдите все пары чисел а и b, при которых наибольшее значение функции у = |х2 + (а - b)х + 2а + b| на отрезке [-3; 1] является наименьшим.
