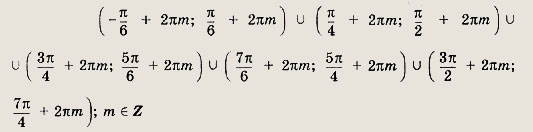БАНК РЕФЕРАТОВ

Тригонометрия

• Тригонометрические функции естественно возникают при рассмотрении метрических соотношений в геометрических задачах. Наличие многочисленных соотношений (формул) между тригонометрическими функциями объясняет их широкое применение. Большое место тригонометрия занимает в школьном курсе математики; без тригонометрии не обходится ни один вступительный экзамен по математике в вуз.
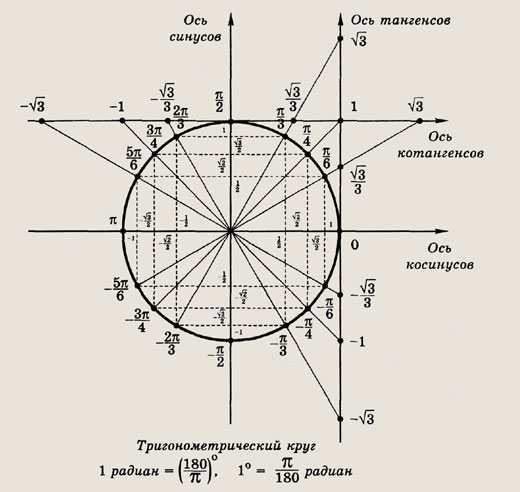
Табличные значения основных тригонометрических функций указаны на тригонометрическом круге.

Используя табличные значения тригонометрических функций, найдите числовые значения выражений (1—10):

Задание 1.

3 cos 0° + 4 sin 90° + 5 tg 180°

Ответ:

7

Задание 2.

4 sin 0° - 5 cos 180° - ctg 90°

Ответ:

5

Задание 3.

4 sin 30° + 5 tg 45° - 2 cos 60°

Ответ:

6

Задание 4.

2 cos 30° - 4 sin 90° + 6 ctg 30°

Ответ:

Задание 5.

Ответ:

1

Задание 6.

Ответ:

Задание 7.

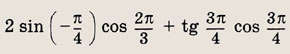
Ответ:

Задание 8.

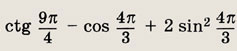
Ответ:

3

Задание 9.

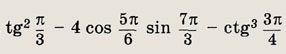
Ответ:

7

Задание 10.

Ответ:

0

 

Используя периодичность тригонометрических функций и формулы приведения:

найдите значения следующих выражений (11—20):

Задание 11.

Ответ:

0

Задание 12.

cos 200° + sin 70°

Ответ:

0

Задание 13.

-sin 380° + cos 110° + 2 sin 20°

Ответ:

0

Задание 14.

sin² 265° + cos2 95°

Ответ:

1

Задание 15.

Ответ:

0

Задание 16.

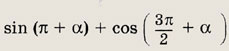
Ответ:

0

Задание 17.

Ответ:

1

Задание 18.

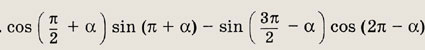
Ответ:

1

Задание 19.

Ответ:

0

Задание 20.

tg 10°tg20° ... tg80°

Решение:

Так как

то tg 80° tg 10° = ctg 10° tg 10° = 1, tg 70° tg 20° = ctg 20° tg 20° = 1 и т. д.

Все сомно жители разбиваются на пары чисел, произведение которых равно единице, поэтому и все произведение — единица.

Ответ:

1

 

Применяя основное тригонометрическое тождество, проверьте выполнение равенств (21—30):

Задание 21.

Задание 22.

Задание 23.

Указание:

Задание 24.

(1 + ctg² ß) sin² ß = 1

Задание 25.

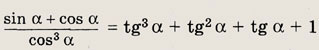
Решение:

Преобразуем левую часть доказываемого равенств; следующим образом:

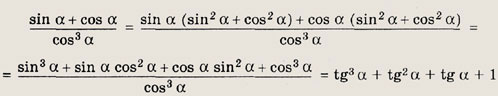
Задание 26.

Задание 27.

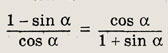
Задание 28.

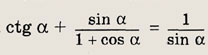
Задание 29.

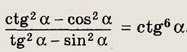
Задание 30.

 

• Приведем основные тригонометрические формулы, на которых основаны все тождественные преобразования тригонометрических выражений.

1)

2)

3)

4)

5)

6)

7)

8)

9)

10)

11)

12)

13)

14)

15)

16)

Соответствующие формулы суммы, разности и произведения для величин

легко получить из их определения и выписанных выше формул. Очень часто бывает полезной формула введения вспомогательного аргумента

17)

где угол

однозначно определяется системой следующих двух равенств:

Используя выписанные формулы, упростите выражения (21—60):

Задание 31.

(sin 23° cos 22° + cos 23° sin 22°) (cos 24° cos 21° - sin 24° sin 21°)

Ответ:

Задание 32.

Ответ:

1

Задание 33.

Ответ:

0

Задание 34.

Ответ:

0

Задание 35.

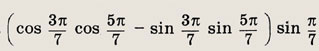
Ответ:

Задание 36.

Ответ:

Задание 37.

Ответ:

Задание 38.

Ответ:

1

Задание 39.

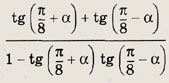
Ответ:

1

Задание 40.

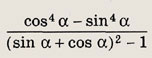
Ответ:

Задание 41.

Ответ:

1

Задание 42.

Ответ:

0

Задание 43.

Ответ:

0

Задание 44.

Решение:

Имеем

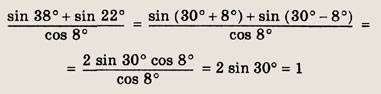
Ответ:

1

Задание 45.

Ответ:

Задание 46.

Указание:

sin 70° - cos 40° = sin 70° - sin 50° = 2 cos 60° sin 10°, a cos 50° + cos 110° = 2 cos 80° cos 30° = 2 sin 10° cos 30°.

Ответ:

Задание 47.

Ответ:

Задание 48.

Ответ:

Задание 49.

2 cos 20° cos 40° - cos 20°

Решение:

Получаем

Ответ:

Задание 50.

sin 10° sin 50° sin 70°

Указание:

Запишите sin 50° = sin (60° - 10°), sin 70° = sin (60° + 10°) и воспользуйтесь формулами синуса суммы и разности углов.

Ответ:

Задание 51.

4 sin 20° sin 40° sin 60° sin 80°

Ответ:

Задание 52.

Ответ:

Задание 53.

Ответ:

Задание 54.

Указание:

Запишите числитель дроби в виде

Ответ:

Задание 55.

Решение:

Имеем

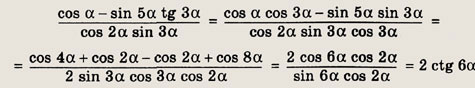
Ответ:

Задание 56.

Решение:

Преобразуем первое слагаемое:

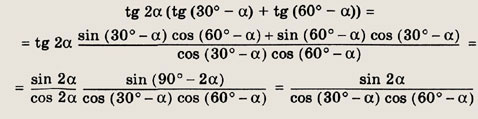
Для второго слагаемого имеем

Суммируя оба слагаемых, получим единицу.

Ответ:

1

Задание 57.

Решение:

Положим

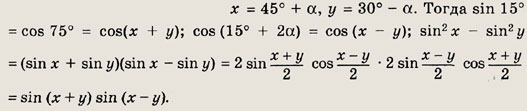
Поэтому данное выражение преобразуется к виду

Ответ:

Задание 58.

Ответ:

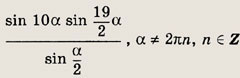
При а = 2Пn, очевидно, искомая сумма равна нулю. Указание. Умножьте и разделите всю сумму на

Задание 59.

Указание:

Умножьте и разделите исхо, ное выражение на

преобразуя полученные произведения косинусов в суммы.

Ответ:

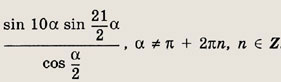
Если же

то искомая сумма равна (-20).

Задание 60.

Решение:

Преобразуем два последних слагаемых, использ5 формулу для тангенса двойного угла. Получаем

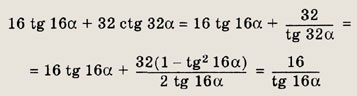
Далее аналогично находим

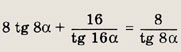
пока не дойдем до последнего шага:

Ответ:

 

Вычислите значения выражений (61—72):

Задание 61.

Решение:

Так как

Поэтому

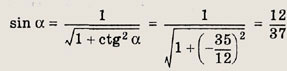
Ответ:

Задание 62.

Указание:

Так как

то

Поэтому

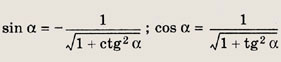
Ответ:

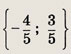
Задание 63.

Ответ:

Задание 64.

Решение:

Так как

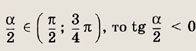
Используя формулу

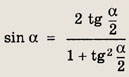
получаем квадратное уравнение для

Ответ:

Задание 65.

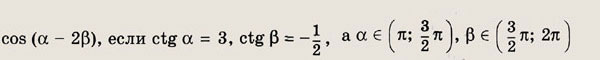
Решение:

Имеем

Учитывая, что

находим

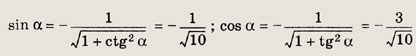
Так как

то

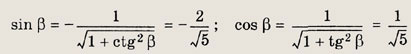
Теперь, вычисляя нужные выражения, получаем

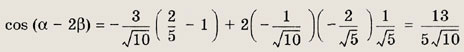
Ответ:

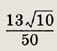
Задание 66.

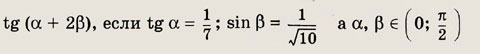
Решение:

Так как

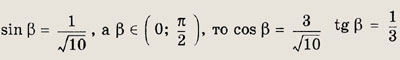
Тогда

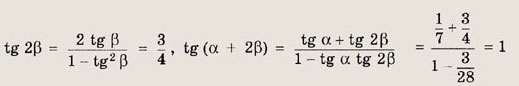
Ответ:

1

Задание 67.

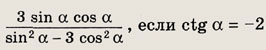
Ответ:

Задание 68.

Ответ:

4

Задание 69.

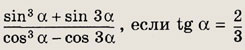
Решение:

Используя формулы

получим

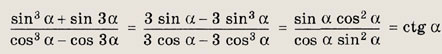
а так как

Ответ:

Задание 70.

Указание:

Возведя равенство

в квадрат, найдите

Далее выразите все искомые величины через

Ответ:

Задание 71.

Решение:

Из уравнения

получаем

Теперь находим

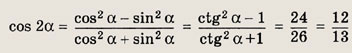
поэтому

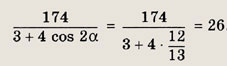
Ответ:

26

Задание 72.

Решение:

Имеем

так как

Если

а в случае

Ответ:

 

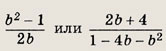
• Напомним следующие определения и тождества, связанные с обратными тригонометрическими функциями.

Арксинус числа х € [-1; 1] (обозначается arcsin x) — это такое число

синус которого равен х.

Таким образом,

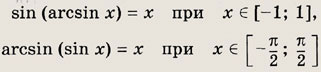
Арккосинус числа х € [-1; 1] (обозначается arccos х) -это такое число у € [0; П], косинус которого равен х. Значит,

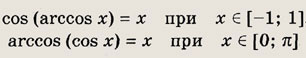
Арктангенс числа х € R (обозначается arctg x) — это такое число

тангенс которого равен х.

Следовательно,

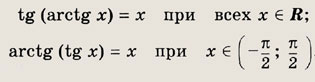
Арккотангенс числа х € R (обозначается arcctg x) — это такое число у 6 (0; П), котангенс которого равен х. Поэтому

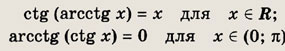
Справедливы также два следующих тождества:

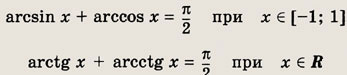
Табличные значения обратных тригонометрических функций

можно найти на тригонометрическом круге (см. рис. выше).

Вычислите значения выражении (73—100):

Задание 73.

Ответ:

Задание 74.

Ответ:

Задание 75.

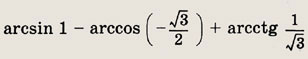
Ответ:

0

Задание 76.

Ответ:

Задание 77.

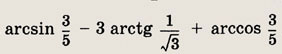
Ответ:

0

Задание 78.

arctg 10 + arcsin 1 + arcctg 10

Ответ:

П

Задание 79.

Решение:

Имеем

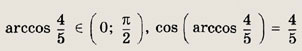
noэтому

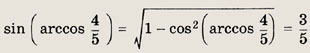
Ответ:

Задание 80.

Ответ:

Задание 81.

sin (arcctg 7)

Ответ:

Задание 82.

Ответ:

Задание 83.

Ответ:

Задание 84.

Ответ:

Задание 85.

Ответ:

Задание 86.

Решение:

Так как

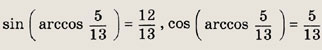
то

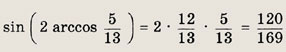
Ответ:

Задание 87.

Ответ:

Задание 88.

Ответ:

Задание 89.

Решение:

Пусть

Тогда

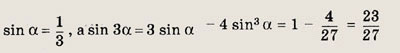
Ответ:

Задание 90.

Ответ:

Задание 91.

Ответ:

Задание 92.

Решение:

Пусть

Тогда

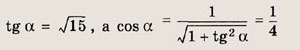
Далее, так как

Ответ:

Задание 93.

Решение:

Находим

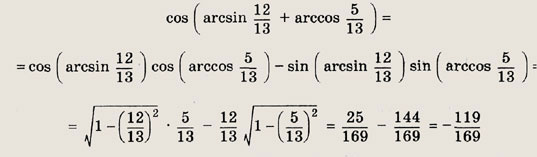
Ответ:

Задание 94.

Ответ:

Задание 95.

Ответ:

Задание 96.

Решение:

Имеем

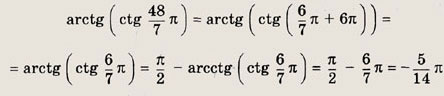
Ответ:

Задание 97.

Ответ:

Задание 98.

Ответ:

Задание 99.

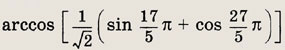
Решение:

Находим

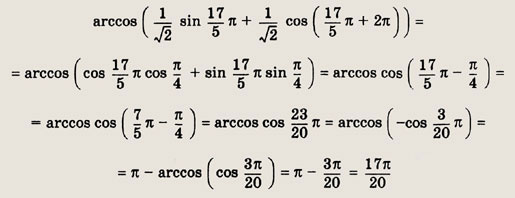
Ответ:

Задание 100.

Указание:

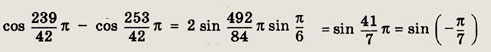
Ответ:

Проверьте выполнение равенств (101—105):

Задание 101.

Решение:

Положим

Тогда

Учитывая, что

Задание 102.

arctg 1 + arctg 2 + arctg 3 = П

Решение:

Пусть

что и доказывает нужное равенство.

Задание 103.

Задание 104.

Задание 105.

Решение:

Имеем

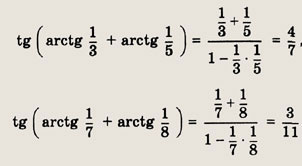
Далее, полагая

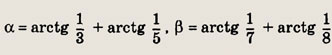
и замечая, что

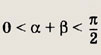
получаем

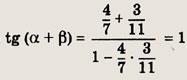
откуда

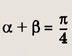
что и требовалось доказать.

 

Постройте графики следующих функций и уравнений (106—129):

Задание 106.

у = sin 2x

Ответ:

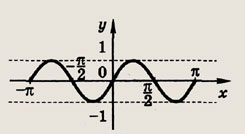
Задание 107.

у = cos Пх

Ответ:

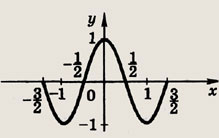
Задание 108.

у - Isin х|

Ответ:

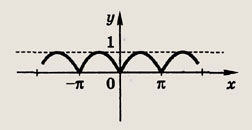
Задание 109.

у = sin |х|

Ответ:

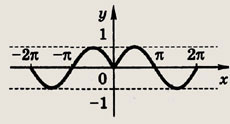
Задание 110.

|у| = cos х

Ответ:

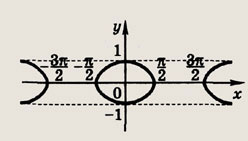
Задание 111.

у = cos х + |cos x|

Ответ:

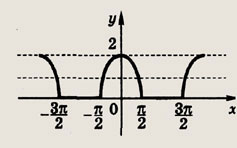
Задание 112.

у = |tg x|

Ответ:

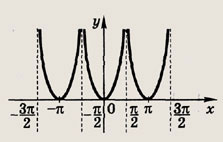
Задание 113.

Ответ:

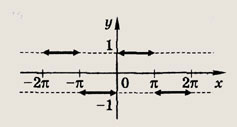
Задание 114.

у = |tg x| cos x

Ответ:

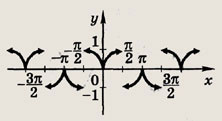
Задание 115.

y = cos²x

Ответ:

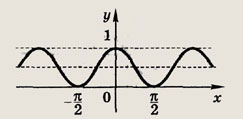
Задание 116.

у = sin x + cos x

Ответ:

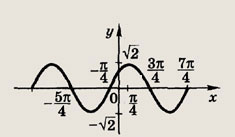
Задание 117.

Ответ:

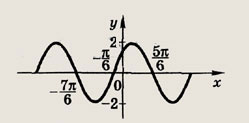
Задание 118.

Ответ:

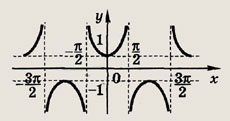
Задание 119.

у = tgx + ctgx

Ответ:

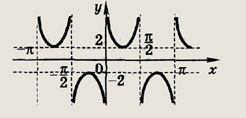
Задание 120.

Ответ:

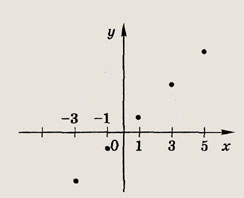
Задание 121.

Ответ:

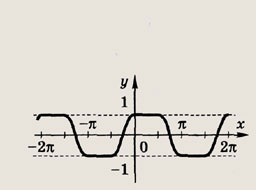
Задание 122.

tg y= tg x

Ответ:

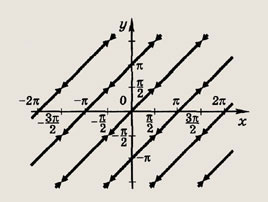
Задание 123.

sin у = sin x

Ответ:

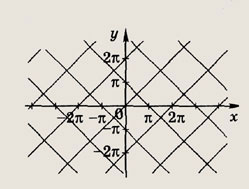
Задание 124.

у = arcsin 2x

Ответ:

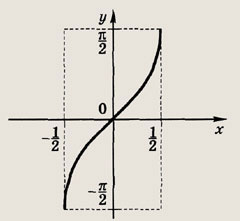
Задание 125.

|y| = arccos x

Ответ:

Задание 126.

у = cos (arccos x)

Ответ:

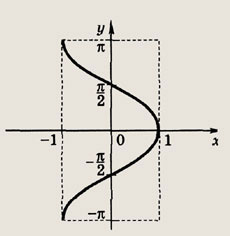
Задание 127.

у - sin (arccos x)

Ответ:

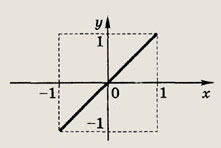
Задание 128.

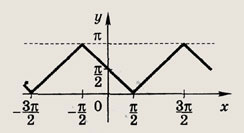
у - arcsin (sin x)

Ответ:

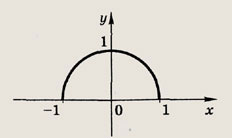
Задание 129.

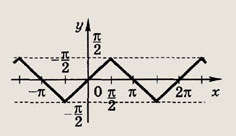
у - arccos (sin x)

Ответ:

 

• Решения следующих простейших тригонометрических уравнений находятся по формулам:

 

Решите простейшие тригонометрические уравнения (130—149):

Задание 130.

Ответ:

Задание 131.

Ответ:

Задание 132.

Ответ:

Задание 133.

Ответ:

Задание 134.

Ответ:

Задание 135.

Ответ:

Задание 136.

Ответ:

Задание 137.

Ответ:

Задание 138.

Ответ:

Задание 139.

Ответ:

Задание 140.

Ответ:

Задание 141.

Ответ:

Задание 142.

Ответ:

Задание 143.

2 cos 3x + cos² 7x = - sin² 7x

Ответ:

Задание 144.

4 cos² Зx = 3

Ответ:

Задание 145.

Ответ:

Задание 146.

2 sin² x = sin x

Ответ:

Задание 147.

2 cos x ctg x + ctg x = 0

Ответ:

Задание 148.

Ответ:

Задание 149.

ctg² x - 2 cos² x = 0

Ответ:

 

Решите уравнения (150—161), сведя их к квадратному уравнению относительно какой-либо функции:

Задание 150.

2 sin²x - 3 sin x + 1 = 0

Ответ:

Задание 151.

tg²x + 4tgx + 3 = 0

Ответ:

Задание 152.

6 sin²x - 5 cos x - 5 = 0

Ответ:

Задание 153.

6 cos² x - 13 sin x - 13 = 0

Ответ:

Задание 154.

Решение:

Так как

то уравнение преобразуется к виду

tg² х + tgх - 2 = 0, откуда tg х= 1, tg х = -2.

Ответ:

Задание 155.

Ответ:

Задание 156.

tg x 3 ctg x = 4

Ответ:

Задание 157.

Ответ:

Задание 158.

sin x - 2 cos 2x = 1

Решение:

Так как cos 2x = 1 - 2 sin²х, то уравнение примет вид 4 sin²х + sin х - 3 = 0, откуда

Ответ:

Задание 159.

cos 2x + 3 cos x + 2 = 0

Ответ:

Задание 160.

Ответ:

Задание 161.

3 + 5 sin 2x = cos 4x

Ответ:

Решите уравнения (162—173), воспользовавшись однородностью левых частей этих уравнений:

Задание 162.

cos x - sin x = 0

Ответ:

Задание 163.

cos x + sin x = 0

Ответ:

Задание 164.

3 cos x + 2 sin x = 0

Ответ:

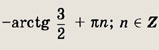
Задание 165.

4 sin x - 5 cos x = 0

Ответ:

Задание 166.

sin² x - sin x cos x - 2 cos²x = 0

Решение:

Разделив на cos² х обе части уравнения, получим равносильное исходному уравнение tg² x-tgx-2 = 0, откуда tg х = -1, tg х = 2.

Ответ:

Задание 167.

4 cos²x - 7 sin x cosx + 3 sin²x = 0

Ответ:

Задание 168.

2 sin² x + 5 sin x cos х + 5 cos² x = 1

Решение:

Записав уравнение в виде

2 sin²х + 5 sin x cos x + + 5 cos2 x = sin² x + cos² х получим

sin² x + 5 sin х cos х + 4 cos² x = 0,

откуда tg² x + 5tgх + 4 = 0. Значит, tg x = -1, tg x = -4.

Ответ:

-arctg 4 + Пk; n, k € Z.

Задание 169.

5 sin²x + 4 sin x cos x - 5 cos²x = 2

Ответ:

Задание 170.

2 sin² x - sin x cos x + 5 cos² x = 2

Решение:

Записав 2 = 2 cos² х + 2 sin² x, приходим к уравнению

3 cos²х - sin x cos x = 0.

Здесь деление на cos² х приводит к неравносильному исходному уравнению! Поэтому решаем уравнение, приравнивая нулю сомножители

cos x (3 cos x - sin x) = 0, cos х = 0 или

3 cos x - sin x = 0.

Решив эти уравнения, получаем ответ.

Ответ:

arctg 3 + Пk; n, k € Z.

Задание 171.

3 sin² x - 4 sin x cos x + cos² x= 3

Ответ:

Задание 172.

6 sin² 2x + 4 cos²2x - 4 sin 4x = 1

Указание:

Применив формулы

sin 4х = 2 sin 2х cos 2х

1 = sin² 2х + cos² 2х, сведите уравнение к однородному.

Ответ:

Задание 173.

3 sin² x + 5 cos² x - 2 cos 2x + 4 sin 2x = 0

Ответ:

В следующих уравнениях (174—188) примените формулы преобразования произведений тригонометрических функций в суммы или сумм в произведения:

Задание 174.

sin 3x - sin x = 0

Ответ:

Задание 175.

cos 3x - cos 5x= 0

Ответ:

Задание 176.

cos x + sin 3x = 0

Решение:

Применив формулу приведения

запишем уравнение в виде

Отсюда либо

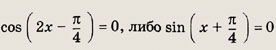
Решив эти уравнения, получаем

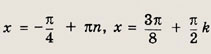
Ответ:

Задание 177.

sin 4x + cos 6x = 0

Ответ:

Задание 178.

sin 2x + sin x + sin 3x = 0

Ответ:

Задание 179.

cos 2x - cos 4x + cos 6x = 0

Указание:

Ответ:

Задание 180.

sin 2x + sin 3x + cos 5x = 1

Решение:

Имеем

Приравнивая каждый сомножитель нулю, получаем ответ.

Ответ:

Задание 181.

1 - sin 2x + cos 2x = sin 4x

Ответ:

Задание 182.

cos x cos 5x = cos 3x cos 7x

Решение:

Преобразуя произведения в суммы, получаем

cos 6х + cos 4х = cos 10х + cos 4х, т. е. cos 10х - cos 6x = 0.

Далее, так как cos 10х - cos 6x = -2 sin 8x sin 2х = 0, то либо sin 8х = 0, либо sin 2х = 0.

Отсюда

Первая серия решений включает вторую.

Ответ:

Задание 183.

sin 3x sin 7x = cos 5x cos x

Ответ:

Задание 184.

cos 5x ctg 3x = sin x

Решение:

Уравнение равносильно системе

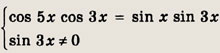
Выполнив преобразования:

2 cos 5х cos Зх = 2 sin x sin Зх, cos 8х + cos 2х = cos 2х - cos 4х, cos 8х + cos 4х = 0,

т. е. 2 cos 6х cos 2х = 0,

получаем решения:

Проверяем, что эти решения удовлетворяют условию: sin Зх # 0. В самом деле,

Ответ:

Задание 185.

tg x cos 5x = sin 7x

Указание:

Учтите, что cos х # # 0.

Ответ:

Задание 186.

tg x - tg 2x = sin x

Решение:

Учитывая, что cos х # 0, cos 2х # 0, преобразуем уравнение к виду

sin x cos 2х - cos x sin 2х = sin x cos cos 2х, т. е.

sin х (1 + cos x cos 2x) = 0.

Отсюда либо sin x = 0, т. е. х = Пn, либо cos 2x cos х + 1 = 0.

Все значения х = Пn, n € Z подходят. Второе уравнение решим, сводя его к кубическому уравнению относительно cos x (другой способ, основанный на ограниченности тригонометрических функций, будет рассмотрен ниже). Так как

cos 2х = 2 cos²x - 1, то 2 cos³ x - cos х + 1 = 0, (cos х + 1)(2 cos² x - 2 cos х + 1) = 0.

Тогда cos х = -1, х = П + 2Пk, k € Z — эти значения подходят, так как принадлежат области определения. Второе уравнение решений не имеет. Объединяя обе серии решений, получаем ответ: х = Пn; n € Z.

Ответ:

х = Пn; n € Z

Задание 187.

tg x cos 3x + sin 3x = 2 sin x

Ответ:

Задание 188.

tg x + tg 2x - tg 3x = 0

Ответ:

Решите уравнения (189—198) методом введения вспомогательного аргумента:

Задание 189.

Ответ:

Задание 190.

Ответ:

Задание 191.

Ответ:

Задание 192.

Задание 193.

3 sin x -- 4 cos x = 5

Решение:

Разделив уравнение на

получим

Пусть

Тогда

и уравнение примет вид

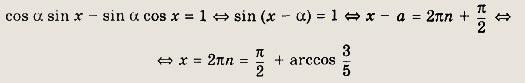
Ответ:

Задание 194.

Ответ:

Задание 195.

12 sin x + 5 cos x = 13 sin 5x

Решение:

Разделим уравнение на

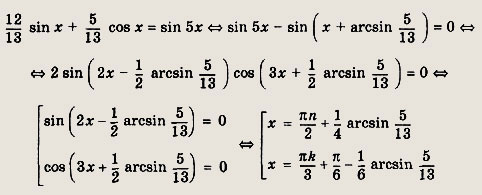
Ответ:

Задание 196.

Ответ:

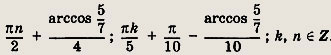
Задание 197.

Ответ:

Задание 198.

Решение:

Так как

то уравнение примет вид

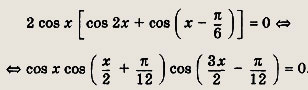
Далее имеем

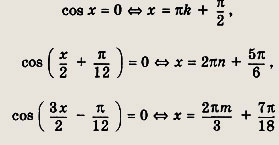
Ответ:

• Уравнения вида

f(sin x cos x; sin x ± cos x) = 0

сводятся к алгебраическому уравнению с помощью замены

t = sin x + cos x (или t = sin x - cos x)

В этом случае

Решите уравнения (199—207):

Задание 199.

1 + sin x cos x = sin x + cos x

Решение:

Пусть sin x + cos x = t. Тогда уравнение примет вид

Таким образом,

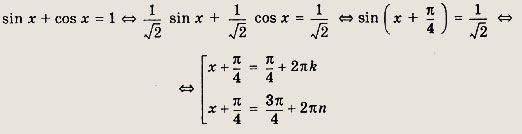
Ответ:

Задание 200.

sin x - cos x = 1 - 3 sin x cos x

Ответ:

Задание 201.

Ответ:

Задание 202.

Ответ:

Задание 203.

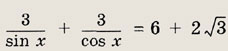
Ответ:

Задание 204.

Решение:

После замены sin х + cos x = t получаем

Это уравнение можно возвести в квадрат, если учесть условие

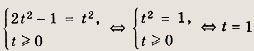
т. е. sin х + cos x = 1, откуда получаем ответ (см. решение задачи 199).

Ответ:

Задание 205.

Ответ:

Задание 206.

sin³ x - cos³ x = 1 - sin x cos x

Решение:

Так как

sin³ x - cos³ x = (sin х - cos x)(sin² x + sin x cos х + cos² x) = = (sin x - cos x)(1 + sin x cos x),

то, полагая sin x - cos x = t, имеем

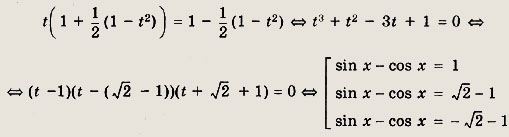
Первое уравнение имеет решения

(см. решение задачи 199.) Третье уравнение не имеет решений, поскольку

Решим второе уравнение:

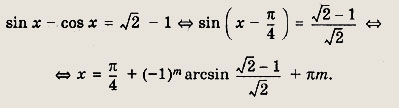
Ответ:

Задание 207.

sin³x + cos³x = 1 + 2 sin 2x

Ответ:

 

Решите уравнения (208—217), воспользовавшись ограниченностью функций у = sin ах и у = cos bx:

Задание 208.

cos 10х + cos 8x = 2

Решение:

Поскольку справедливы оценки

данное уравнение имеет место, если одновременно

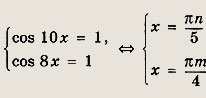
Левые части последних уравнений одинаковы, значит, равны и правые:

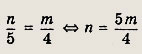
Так как n — целое число, то m делится на 4, т.е. имеет вид m = 4k, откуда n = 5k. Подставляя эти значения в систему, получаем x = Пk.

Ответ:

Пk; k € Z.

Задание 209.

sin 5x - sin 3x = 2

Ответ:

Задание 210.

3 cos² x + 5cos²7x =8

Ответ:

Пn; n € Z.

Задание 211.

5 sin² x - 2 sin11x = 7

Ответ:

Задание 212.

sin x cos 2x = -1

Решение:

Произведение sin x cos 2x может быть равным (-1), если оба сомножителя по модулю равны 1 и противоположны по знаку, т. е. возможны два случая:

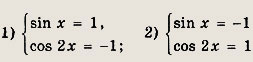
Поскольку cos 2x = 1 - 2 sin² х, вторая система решений не имеет, а в первой системе подходит любое значение х, при котором sin x = 1, т. е.

Ответ:

Задание 213.

cos x cos 2x cos 4x = 1

Ответ:

2Пk; k € Z.

Задание 214.

Решение:

Для существования левой части уравнения необходимо выполнение условий

и кроме того, из неравенств

следует

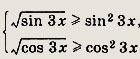
Так как одновременно должны выполняться два равенства

то неравенства превращаются в равенства, поэтому sin Зх и cos Зх могут принимать только два значения: 0 и 1. Это возможно при

Ответ:

Задание 215.

sin⁷ x + cosbx = 1

Ответ:

Задание 216.

sin⁴ x + 2 cos³ x + 2 sin² x - cos x + 1 = 0

Решение:

Запишем уравнение следующим образом:

(sin² х + 1)² = cos x (1 - 2 cos² х), или (sin² x + 1)² = -cos x cos 2x. (*)

Левая часть уравнения может принимать любые значения от 1 до

а правая часть всегда меньше или равна 1

Отсюда следует, что равенство (*) может выполняться только, если одновременно выполняются равенства

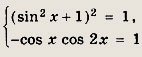
Это может произойти в двух случаях:

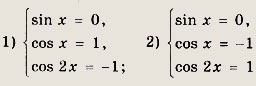
Первая система несовместна, так как если sin х = 0, то cos 2х = 1 - 2 sin² х = 1. Решениями второй системы являются значения х = 2Пk + П.

Ответ:

2Пk + П; k € Z

Задание 217.

2 cos³ x - sin⁴ x - cos x - 2 sin² x = 1

Ответ:

2Пk, гдеk € Z

Используя различные методы, решите следующие уравнения (218—267):

Задание 218.

sin⁴ x - 3 sin² x + 2 = 0

Ответ:

Задание 219.

4 cos⁴ x + 5 cos² x - 6 = 0

Ответ:

Задание 220.

4 cos 2x = ctg² x - 1

Решение:

Так как

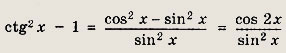
то уравнение принимает вид

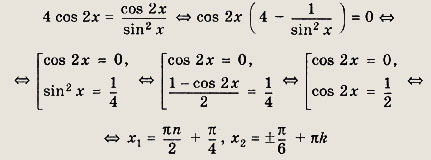
Ответ:

Задание 221.

4 sin 2x = (1 + ctg² x) cos x

Ответ:

Задание 222.

8 sin 2x = tg x + ctg x

Ответ:

Задание 223.

Ответ:

Задание 224.

Решение:

Найдем область определения уравнения:

Теперь, умножив левую и правую его части на (1+2 sin х), получим

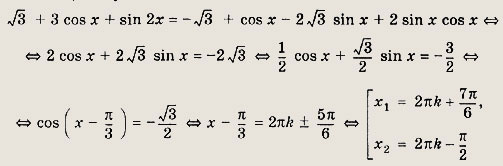
Так как

то корень x₁ не входит в область определения.

Ответ:

Задание 225.

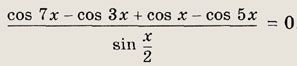
Ответ:

Задание 226.

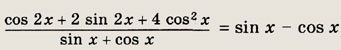
Ответ:

arctg 3 + Пk; k € Z

Задание 227.

Ответ:

arctg (-3) + Пk; k € Z

Задание 228.

tg x (tg x - 2) + ctg x (ctg x - 2) = 6

Решение:

Преобразуем левую часть уравнения:

(tg² x + ctg² x) - 2(tg x + ctg x) = 6 <=> (tg х + ctg х)² - 2(tg x + ctg x) - 8 = 0.

Положим tg x + ctg х = у; тогда получим

у² - 2у - 8 = 0; у₁ = 4, у₂= -2.

Если

Если у = -2, то tg x + ctg x = -2 <=> tg2х + 2 tgх + 1 = 0 <=> tg х = -1,

Заметим, что в случае у = 4 уравнение tg x + ctg x = 4 можно решать по-другому:

Ответ:

Задание 229.

Ответ:

Задание 230.

Решение:

Так как

sin⁴х⁴ - cos⁴ х = (sin²х + cos² х)² - 2 sin²х cos² х,

то уравнение можно преобразовать следующим образом:

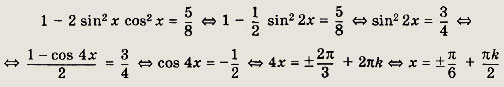
Ответ:

Задание 231.

sin⁴ x + cos⁴ x = sin x cos x

Ответ:

Задание 232.

3 cos⁴ x + sin⁴ x + 2 sin² x cos² x - cos² x = 1

Решение:

Поскольку

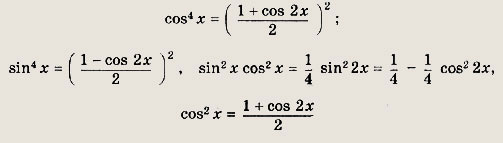
уравнение примет вид

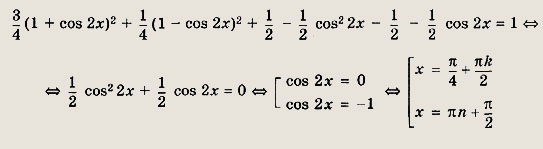
Ответ:

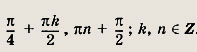
Задание 233.

4 cos⁴ x - 3 sin⁴ x + sin² x cos² x + 3 sin² x = 4

Ответ:

Пk, где k € Z

Задание 234.

2 cos⁴ x + 6 sin ⁴ x - 5 sin ² x + cos² x = 1

Ответ:

Задание 235.

cos⁶ x + sin⁶ x + 3 cos⁴x + 2 sin⁴ x + cos² x = 2

Ответ:

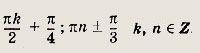
Задание 236.

Решение:

Так как

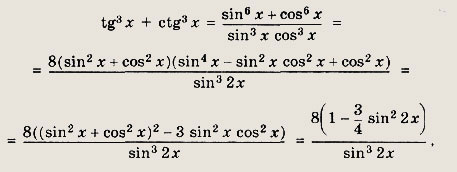
то уравнение принимает вид

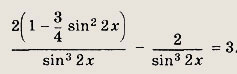
Далее, учитывая область определения (sin 2x # 0), имеем

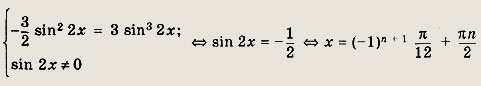
Ответ:

Задание 237.

ctg³ x - tg³ x - 8 ctg² 2x = 6

Решение:

Проведя преобразования, аналогичные тем, что были выполнены при решении предыдущей задачи, получаем

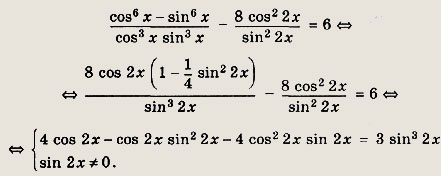
Поскольку cos 2x = cos 2x (sin² 2x + cos² 2х) = sin² 2x cos 2х + cos³ 2x,

уравнение сводится к однородному:

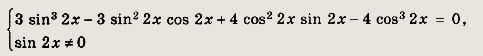
Разделив уравнение на cos³ 2х, имеем

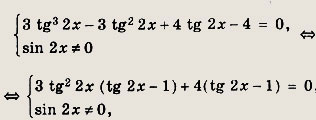
откуда получаем

причем все решения удовлетворяют ограничению sin 2х # 0.

Ответ:

Задание 238.

Решение:

Данное уравнение можно возвести в квадрат при условии, что его правая часть неотрицательна:

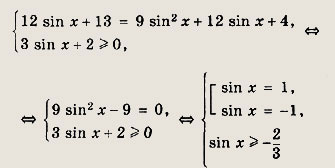
Указанному ограничению удовлетворяет только значение sin x = 1, т.е.

Ответ:

Задание 239.

Ответ:

2Пn, где n € Z

Задание 240.

Ответ:

Задание 241.

Ответ:

Задание 242.

Решение:

Данное уравнение равносильно системе

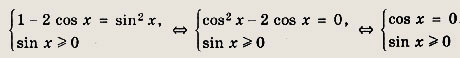
Изобразив решения уравнения cos x = 0 на тригонометрическом круге,

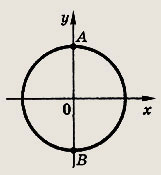
получим точки А и В, причем значения синуса углов, соответствующих точке А, положительны, а углов, соответствующих точке В, отрицательны.

Точке А соответствуют углы

Ответ:

Задание 243.

Ответ:

Задание 244.

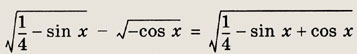
Решение:

Учитывая, что

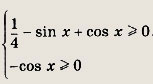
а тогда и

перепишем уравнение в виде

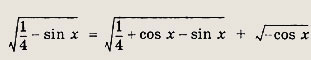
Далее, возведя обе части в квадрат, получаем

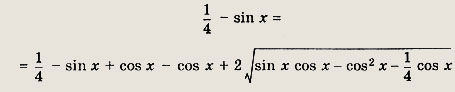
откуда

Решаем уравнение cos x = 0 с учетом того, что

и получаем

Далее,

откуда

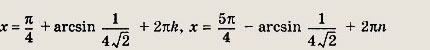
Первая серия не удовлетворяет условию

а вторая удовлетворяет.

Ответ:

Задание 245.

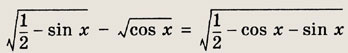
Ответ:

Задание 246.

Решение:

Заметив, что

и возведя обе части равенства в квадрат, получаем

Выполним преобразования:

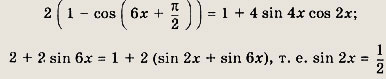
Отсюда либо

Отбираем только те значения х, которые удовлетворяют неравенству

Имеем:

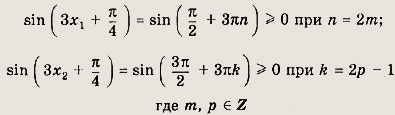
Ответ:

Задание 247.

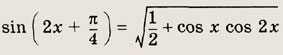
Ответ:

Задание 248.

Решение:

Отметив, что sin Зх # 0, sin х # 0, преобразуем уравнение:

sin² Зх - sin² х = 2 sin x sin Зх cos 2х;
(sin Зх- sin x)(sin Зх + sin х) = 2 sin х sin Зх cos 2х;
4 sin х cos 2х sin 2х cos х = 2 sin х sin Зх cos 2x;
sin х cos 2х (2 sin 2х cos х - sin Зх) = 0,

откуда, учитывая, что sin Зх = sin 2х cos х + cos 2х sin х, получаем

sin² х cos 2х = 0.

Поскольку решения sin х = 0 не принадлежат области определения, решениями уравнения являются те значения х, для которых

Все эти решения входят в область определения.

Ответ:

Задание 249.

Ответ:

Задание 250.

Указание:

Сведите уравнение к квадратному относительно cos 2х.

Ответ:

Задание 251.

2 sin² x = 4 sin³ 2x + 7 cos 2x - 6

Ответ:

Задание 252.

2П cos x = |x| - |x - П|

Решение:

Рассмотрим три случая.

1) х < 0. Уравнение примет вид

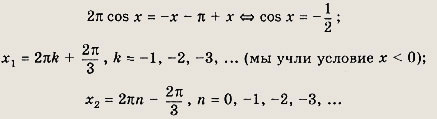
2) х > П. Уравнение имеет вид

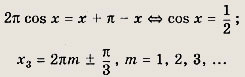
3)

Получаем уравнение

Так как функция у = cos х монотонно убывает на отрезке [0; П], а функция

монотонно возрастает на том же отрезке и, кроме того,

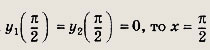
—единственное решение уравнения

Ответ:

Задание 253.

Ответ:

Задание 254.

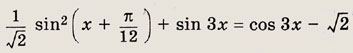
Решение:

Преобразуем уравнение:

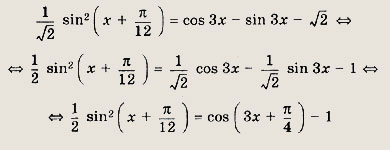
Поскольку левая часть уравнения неотрицательна, а правая не положительна, равенство возможно, если обе части уравнения одновременно обратятся в нуль, т.е.

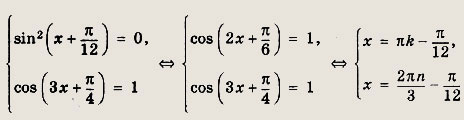
Общими являются решения

Ответ:

Задание 255.

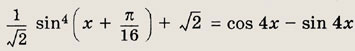
Ответ:

Задание 256.

sin (ЗП cos x) = cos (4П sin x)

Решение:

Преобразуем уравнение так:

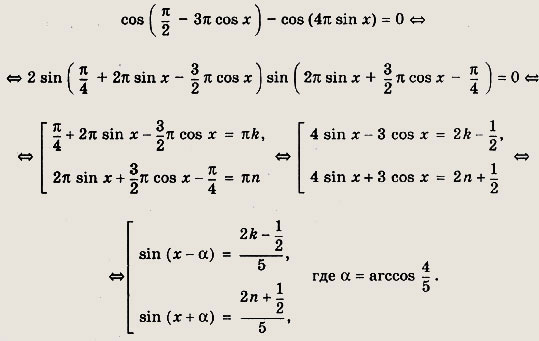
Эти уравнения имеют решения, если справедливы неравенства

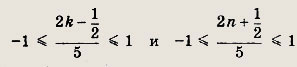
которые выполняются при k, n € {0; ±1; ±2}.

Ответ:

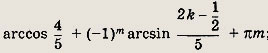
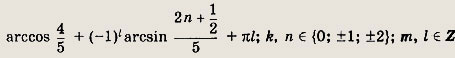
Задание 257.

tg (П sin x) - ctg (П cos x)

Ответ:

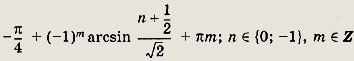
Задание 258.

Решение:

Так как

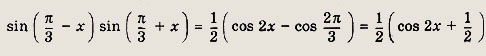
то исходное уравнение примет вид

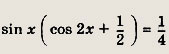
Учитывая, что

приходим к уравнению

откуда

Ответ:

Задание 259.

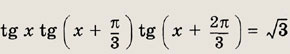
Ответ:

Задание 260.

2 tg Зх - 3 tg 2x = tg² 2x tg 3x

Решение:

Запишем исходное уравнение в виде

2(tg Зх - tg 2x) = = tg 2х (1 + tg 2x tg Зх), откуда, используя тождества

получим уравнение

Оно распадается на совокупность уравнений sin х = 0 и cos 2x = 1, решениями которых являются х = Пn.

Ответ:

Пn, n € Z

Задание 261.

tg x tg 2x tg 3x = tg 3x - tg 2x - tg x

Решение:

Умножим обе части уравнения на cos x cos 2x cos Зх (при этом в конце решения надо будет учесть, что эти множители не равны нулю). Получим

sin x sin 2x sin Зх = sin Зх cos 2x cos x - sin 2x cos Зх cos x - sin x cos 2x cos Зх <=>
<=> sin x (sin 2x sin Зх + cos 2x cos Зх) == cos x (sin Зх cos 2x - sin 2x cos 3x).

sin x cos x = sin x cos x — тождество. Оно выполняется при всех ж из области определения (cos x, cos 2x, cos Зх # 0).

Ответ:

где

Задание 262.

Решение:

Умножим левую и правую части уравнения на

(при этом, возможно, появятся лишние решения

т. е. х = 4Пm). Имеем

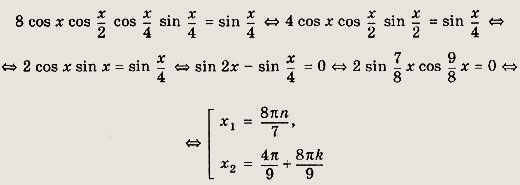
Решения x = 4Пm — действительно лишние (подставьте эти значения х в исходное уравнение).

Ответ:

n, k, p € Z

Задание 263.

8 cos x cos 2x cos 4x cos 8x: = cos 15x

Ответ:

Задание 264.

Решение:

Данное уравнение эквивалентно системе

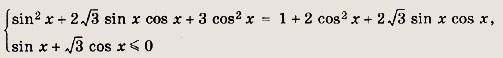
Полученное уравнение представляет собой тождество. Решаем неравенство:

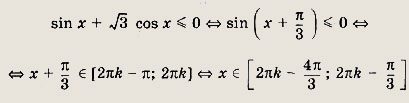
Ответ:

Задание 265.

Ответ:

Задание 266.

Решение:

Положим

Тогда

а уравнение примет вид 6 cos у - 1 = |sin y|. Поскольку правая часть неотрицательна, то же самое относится к левой части. Поэтому можно возвести в квадрат:

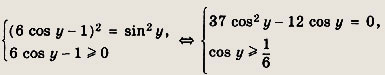
Из уравнения имеем

— , причем первое значение косинуса не удовлетворяет неравенству. Таким образом,

Ответ:

Задание 267.

2 sin 2x - sin x - sin 3x + |1 - 2 cos х + cos 2x | = 0

Решение:

Применив формулы суммы синусов и косинуса двойного угла, получаем

2 sin 2х - 2 sin 2x cos х + |1 - 2 cos х + 2 cos²х - 1| = 0 <=>
<=> 2 sin 2х (1 - cos х) + |2 cos x (cos x - 1)| = 0 <=>
<=> sin 2х (1 - cos х) + |cos x| (1 - cos х) = 0 <=>
<=>(1 - cos x) (sin 2x* + |cos x|) = 0.

Отсюда либо cos х = 1, т. е. х = 2Пk, k € Z, либо |cos x| = -2 sin x cos x. Последнее уравнение равносильно совокупности соотношений:

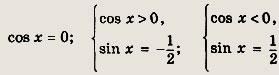
Решив эти уравнения, получим

Ответ:

 

Решите уравнения, содержащие обратные тригонометрические функции (268—280):

Задание 268.

Указание:

Воспользуйтесь тождеством

Ответ:

{1}

Задание 269.

7 arcsin x + arccos x = 2П

Ответ:

Задание 270.

Решение:

Легко проверить, что

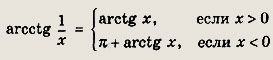
Тогда получим

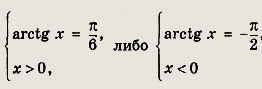
Первая система дает

а вторая не имеет решений, так как

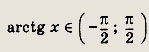
Ответ:

Задание 271.

Указание:

Покажите, что

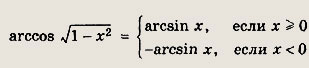
Ответ:

Задание 272.

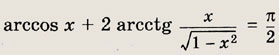
Решение:

Воспользуемся равенством

и получим, что

Отсюда

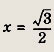
Ответ:

Задание 273.

Решение:

Решив квадратное уравнение, получаем

либо

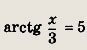
Второе равенство невозможно, так как

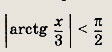
Если

Ответ:

-3 tg 1

Задание 274.

3 arctg² x - 4П arctg x + П² = 0

Ответ:

Задание 275.

6 arcsin² x + 2П arccos x - П² = 0

Указание:

Воспользуйтесь тем, что

Ответ:

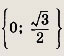
Задание 276.

Ответ:

2

Задание 277.

2 arcsin 2x = arccos 7x

Решение:

Заметив, что

и взяв косинус от обеих частей равенства, получим 1 - 8х² = 7х, так как cos 2а = 1 - 2 sin² а. Отсюда

(посторонний корень).

Ответ:

Задание 278.

Решение:

Область определения уравнения задается условием

На этом множестве правая часть уравнения неположительна, а функция

— всегда неотрицательна, поэтому уравнение имеет решение только если

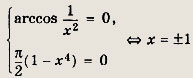
Ответ:

{±1}

Задание 279.

Ответ:

{±1}

Задание 280.

Решение:

Преобразуем левую часть уравнения:

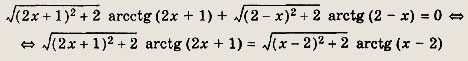
Функция

является монотонно возрастающей. Равенство означает, что значения функции при t₁ = 2х + 1 и t₂ = х - 2 совпадают, что может произойти только если t₁ = t₂<=> х = -3.

Ответ:

-3

Решите следующие системы (281—292):

Задание 281.

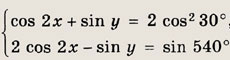
Решение:

Преобразуем уравнения системы:

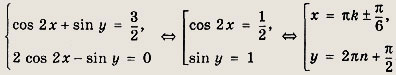
Важно, что буквы k и n разные!

Ответ:

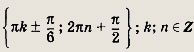
Задание 282.

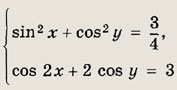
Решение:

В силу ограниченности косинуса второе уравнение системы имеет место только при условиях

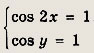
Если же подставить значение cos у = 1 в первое уравнение исходной системы, то получим

чего не может быть. Отсюда следует, что система несовместна (не имеет решений).

Ответ:

0

Задание 283.

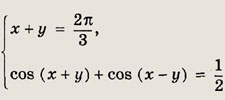
Решение:

Из первого уравнения имеем

Подставим это выражение у во второе уравнение:

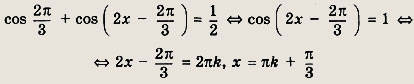
Тогда из первого уравнения следует, что

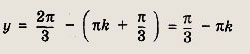
Ответ:

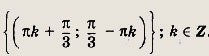
Задание 284.

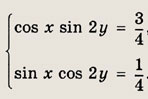
Решение:

Сложив уравнения, находим sin (х + 2у) = 1. Если вычесть из первого уравнения второе, то получим

Таким образом,

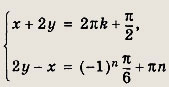
откуда

Заметим, что в этом случае важно, что k и n — разные буквы.

Ответ:

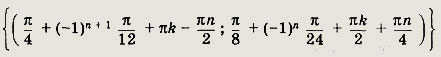
k, n € Z

Задание 285.

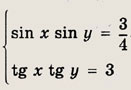
Ответ:

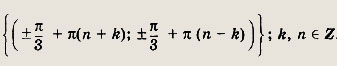
Задание 286.

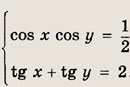
Решение:

Второе уравнение системы перепишем в виде

откуда, используя первое уравнение, получим

Тогда

и первое уравнение примет вид

Ответ:

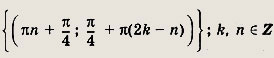
Задание 287.

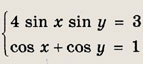
Ответ:

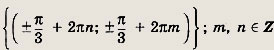
Задание 288.

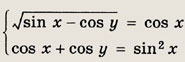
Решение:

Учитывая условие

возведем первое уравнение в квадрат:

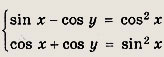
Сложив уравнения, получаем

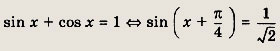
откуда

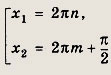
Подставляя эти значения х во второе уравнение исходной системы, находим

cos У₁ = -1, У₁ = 2Пk + П;
COS у₂ = 1, У₂ = 2Пр.

Ответ:

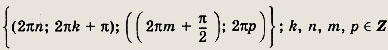
Задание 289.

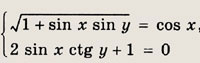
Ответ:

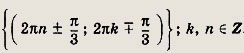
Задание 290.

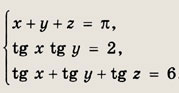
Решение:

Из первого уравнения выразим z = П - х - у, откуда tg z = -tg (x + у). Для нахождения х и у получаем систему

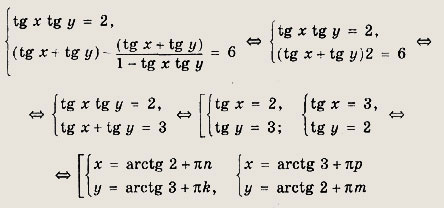
Значения z получаем из соотношения z = П - х - у.

Ответ:

{(arctg 2 + Пn; arctg 3 + Пk; -arctg 2 - arctg 3 + П(1 - n - k)) (arctg 3 + Пр; arctg 2 + Пm; -arctg 2 - arctg 3 + П(1 - p - m))}; k, n, p, m € Z

Задание 291.

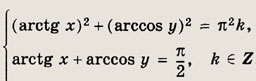
Решение:

Полагая arctg л: = u, arccos у = v, приходим к системе

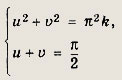
решив которую получаем

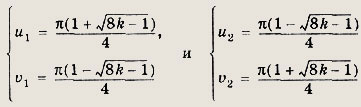
Так как

то подходят только решения второй серии при k = 1.

Ответ:

Задание 292.

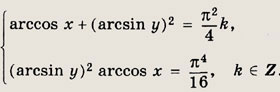
Ответ:

 

Решите задачи (293, 294) с учетом ограниченности функций синус и косинус.

Задание 293.

Найдите наименьшее значение выражений:

а) 4 sin² x + 12 sin x + tg²y - 6 tg у;

б) ctg² х + 4 ctg x + cos² у - 6 cos у

Решение а):

Преобразуем данное выражение:

где

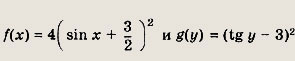
Поскольку sin x € [-1; 1], минимальное значение ƒ(х) равно

Минимальное значение g(y) достигается при tg у = 3 и равно нулю.
Таким образом, минимальное значение f(x) + g(y) - 18 равно 1 + 0 - 18 = -17.

Ответ:

a) -17

б) -9

Задание 294.

Найдите наименьшее значение функций:

а) у = (arccos x)² - 2a arccos x + а² - 1

б) у = (arcsin x)² - (2b + 1) arcsin x + b² + b - 2

Решение а):

Так как выражение arccos x может принимать любые значения из отрезка [0; П], то задача сводится к нахождению минимума функции f(x) = (t - а)² - 1 на отрезке [0; П]. Рассмотрим три случая:

1) а 6 [0; П]. Наименьшее значение f(t) на отрезке [0; П] достигается в точке t = а. При этом f(a) = -1;

2)

Функция f(t) монотонно возрастает на отрезке [0; П] и min_[0;П]f(t) =f(0) = a²- 1;

3)

Функция f(t) монотонно убывает на [0; П]. Таким образом, min_[0;П]f(t) = f(П) = (П - а)² - 1.

Ответ:

a)

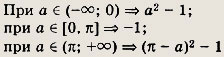
b)

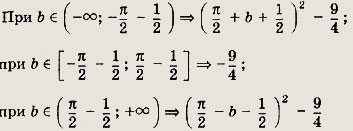
Задание 295.

При каких значениях параметра а уравнение

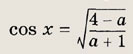
имеет на отрезке

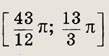
два различных решения?

Решение:

Поскольку функция cos x является периодической с периодом 2П, отрезок

можно заменить на

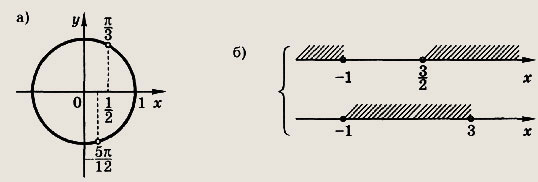
Уравнение cos x = p имеет ровно два решения на этом отрезке, если

Таким образом, нужные значения а являются решениями неравенства

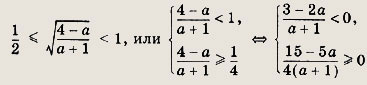
Обоим множествам удовлетворяют значения

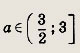
Ответ:

Задание 296.

При каких значениях параметра а уравнение

2 sin² Зx - (2а + 1) sin Зх + а = 0

имеет на отрезке

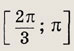
ровно три различных решения?

Ответ:

а = 1

Задание 297.

Найдите все значения параметра а, при которых уравнение

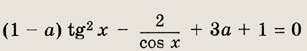
имеет на интервале 0; - более одного решения.

Решение:

Положим

Тогда получим квадратное уравнение относительно t:

(1 - a)t² - 2t + 4а = 0.

Для того чтобы исходное уравнение имело два корня на интервале

необходимо и достаточно, чтобы уравнение имело ровно два корня, больших 1.

Решив это уравнение относительно t, получаем

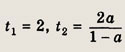
Условие

При этом надо отбросить случай

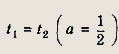
Замечание. При а = 1 уравнение не является квадратным Этот случай надо рассмотреть отдельно.

Ответ:

Задание 298.

При каких значениях параметра а уравнение

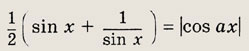
имеет решения?

Решение:

Из вида уравнения заключаем, что sin x > 0. Тогда

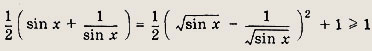
a

Равенство возможно только в том случае, если

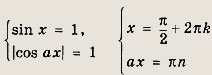
откуда

где n, k € Z.

Ответ:

Задание 299.

При каком наибольшем значении

принадлежащем отрезку

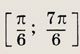
корни x₁ и х₂ уравнения

удовлетворяют равенству x₁^-2 + х₂^-2 =8?

Решение:

При

корни уравнения существуют, так как в этом случае дискриминант

Используя теорему Виета, получим

откуда

Эти уравнения имеют решения

из которых на отрезке

лежат только

Ответ:

П

Задание 300.

Найдите все значения

при которых больший корень уравнения

на

больше, чем квадрат разности корней уравнения

Решение:

Вычисляя больший корень первого уравнения

получаем

Второе уравнение имеет корни при всех

так как его дискриминант

Применяя теорему Виета, находим разность корней этого уравнения:

Таким образом, нужно решить уравнение

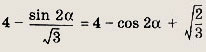
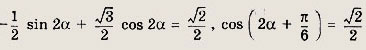
откуда

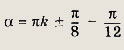
Ответ:

Задание 301.

Найдите все значения а, при которых меньший корень уравнения

равен сумме квадратов корней уравнения

Ответ:

Задание 302.

При каких значениях параметра а имеют решения уравнения:

а) sin² х + a sin х + 1 - а² - 0

б)

Указание:

Полагая sin x = t и учитывая, что

сведите задачу к исследованию квадратного трехчлена у = t² + at + 1 - а². Теперь нужно установить, при каких а этот трехчлен имеет хотя бы один корень на отрезке [-1; 1].

Решение б:

Полагая

приходим к системе уравнений

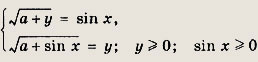
Возведя уравнения в квадрат и вычитая из первого равенства второе, получим

у - sin x = sin² x - у²; (у - sin x) (у + sin x + 1) = 0, откуда у = sin x. Равенство у + sin x + 1 = 0 невозможно, так как

и

Мы получили уравнение

при условии

Находим

Для того чтобы исходное уравнение имело решение, достаточно выполнения хотя бы одной из следующих систем неравенств:

В обоих случаях получаем, что

Ответ:

а)

b)

 

Решите следующие уравнения (303—316):

Задание 303.

4 sin 2х + a cos х = cos Зх

Указание:

Используйте формулы sin 2х = 2 sin x cos x, cos За: = 4 cos³ х - 3 cos x.

Ответ:

при

при

Задание 304.

2 sin 2х - a² sin x + sin 3x = 0

Решение:

Получаем:

4 sin х cos х - a² sin x + 3 sin x - 4 sin³ х = 0; sin x [4 cos х-а²+ 3-4(1- cos² x)] = 0;
sin x [4 cos² х + 4 cos x - (а² + 1)] = 0,

откуда sin x = 0, т. е. х = Пn при любом а € R и, либо 4 cos² x + 4 cos x - (а² + 1) = 0. В этом случае

Второе решение — постороннее

а первое имеет смысл в том случае, если

Ответ:

при

при

Задание 305.

cos⁴x - (а + 2) cos²x - (а + 3) = 0

Ответ:

при

при других

Задание 306.

sin⁴ x + (а - 5) sin²x - 2(а - 3) = 0

Ответ:

при

при других

Задание 307.

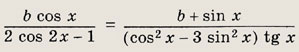
Ответ:

при

при

Задание 308.

Решение:

При условиях cos х # 0, cos 2x # 0 уравнение преобразуется к виду

Условие cos х # 0 влечет

т. е. а # ±1. Условие cos 2х = 1 - 2 sin² х # 0 влечет, что

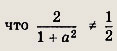
т. е.

Наконец, при а € (-1; 1) само уравнение

не будет иметь решений.

Ответ:

при

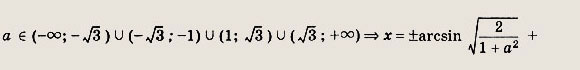
при

Задание 309.

Решение:

Преобразуя обе части уравнения, получаем

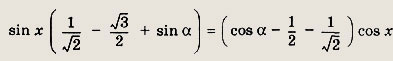
Так как

откуда

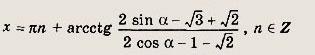
Ответ:

Задание 310.

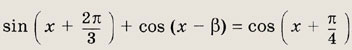
Ответ:

при

при

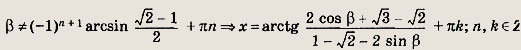
Задание 311.

Решение:

Используя метод введения вспомогательного аргумента, получаем

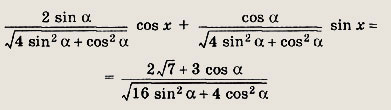
Так как теперь выражение слева можно быть записать в виде

— соответствующий вспомогательный угол, то дл существования решения должно выполняться условие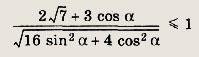

(очевидно, что

). Решим это неравенство. Получаем

откуда

Значит, уравнение может иметь решение только при

Возможны следующие два случая:

1)

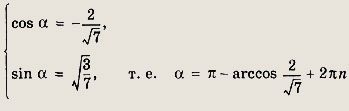
Подставляя эти значения

в исходное уравнение, получим

Таким образом, при

2)

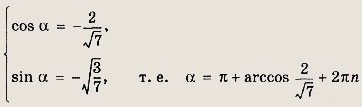
Теперь исходное уравнение преобразуется к виду

т. е.

Ответ:

при

при

при других

Задание 312.

Ответ:

при

при

при других

Задание 313.

|3 sin x - a + 1| = 2 sin x - 4a + 7

Ответ:

при

при

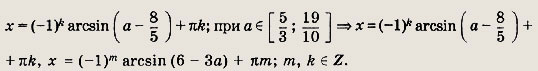
Задание 314.

|2 cos x - a| - 2a = 3 cos x + 1

Ответ:

при

при

при

n, k € Z

Задание 315.

Ответ:

при

при а = 0 =* х => Пm; при

Задание 316.

Указание:

См. задачу 302,б.

Ответ:

при

при

Задание 317.

Решите неравенства:

а)


б)

Решение а):

Записав неравенство в виде

видим, что

Отсюда очевидно, что неравенство выполняется лишь при у = 1 и х = 0.

Ответ:

а) (0; 1)

б) (0; 1)

Задание 318.

Найдите все значения параметра b, при котором все корни уравнения

(х + 1)[2 cos 4х - 2 + 8(b - 3) sin x cos x + 5b(b - 4)] + 19x = -19

не превосходят единицу.

Решение:

Запишем уравнение в виде

(х + 1) [4 sin² 2х - 4(6 - 3) sin 2х - (5b² - 206 + 19)] = 0.

Одно из решений, х = - 1 удовлетворяет условию задачи. Все другие решения — это решения тригонометрического уравнения

4 sin² 2х - 4(6 - 3) sin 2х - (562 - 206 + 19) = 0.

Если Х₀ — решение этого уравнения, то и любое число вида х₀ + Пk, k € Z также будут решениями уравнения, а значит, среди них обязательно найдутся решения, большие 1. Полагая sin 2x = t и заметив, что

приходим к следующей задаче: нужно найти b € N, при которых уравнение

4t² - 4(6 -3)( - (562 - 206 + 19) = 0

не имеет решений, принадлежащих отрезку [-1; 1]. Для этого уравнения

- уравнение решений не имеет (D < О), следовательно, эти значения удовлетворяют условию задачи.

Если

то

причем

Теперь, решив неравенства

находим, что при

также выполнены условния задачи.

Ответ:

Задание 319.

Найдите все значения параметра а, при котором все корни уравнения

отрицательные.

Ответ:

Задание 320.

При каких действительных х для любого действительного у найдется такое z, что

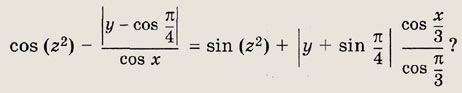
Указание:

Далее см. решение задачи 321.

Ответ:

ЗПk ± П; k € Z

Задание 321.

При каких действительных х для любого действительного у найдется такое z, что

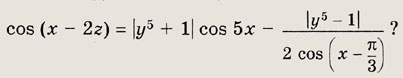
Решение:

Так как по условию уравнение должно иметь решение для любого действительного у, то при у = -1 получаем

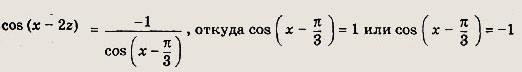
Решив эти уравнения, находим

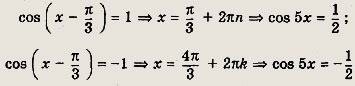
При

исходное уравнение примет вид

Полагая y⁵ = t, заключаем, что функция

при всех t принимает значения на [-1; 1]. Ее график изображен на рис.

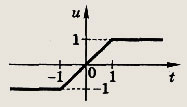
Тогда при любом у € R уравнение

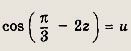
будет иметь решения. Аналогично, если

то уравнение примет вид

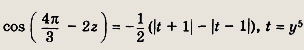
и также имеет решения при любом у € R.

Ответ:

Задание 322.

При каких неотрицательных значениях а все неотрицательные решения уравнения

cos (6а - 3)х = cos (12а + 5)х,

расположенные в порядке возрастания, образуют арифметическую прогрессию?

Решение:

Решив данное уравнение, получим

По условию

Решения неотрицательны при

При n = k = 0 оба корня равны нулю. Для того чтобы все неотрицательные корни составляли арифметическую прогрессию (т. е. располагались по числовой оси на равных расстояниях друг от друга) необходимо выполнение условий

где p,q € N. В первом случае

а во втором

а₆ = 0

Ответ:

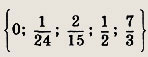
Задание 323.

При каких положительных значениях а все неотрицательные решения уравнения

cos (8а - 3)х = cos (14а + 5)х,

расположенные в порядке возрастания, образуют арифметическую прогрессию?

Ответ:

 

Решите тригонометрические неравенства (324—336):

Задание 324.

Ответ:

Задание 325.

Ответ:

Задание 326.

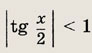
Решение:

Имеем

Заметим, что справа и слева в неравенстве должна стоять одна и та же буква, отмечающая период. Окончательно получаем

Ответ:

Задание 327.

Указание:

Замените cos 2х = 1 - 2 sin² x и решите сначала квадратичное неравенство для функции sin х.

Ответ:

Задание 328.

Указание:

Воспользуйтесь тем, что

решите сначала неравенство

Ответ:

Задание 329.

Решение:

Неравенство равносильно системе

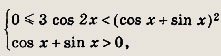
откуда, учитывая, что cos 2x = (cos x + sin x) (cos x - sin х), имеем

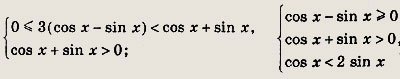
Отсюда легко получим, что

Следовательно,

Ответ:

Задание 330.

Решение:

Пусть cos х - sin x = t. Тогда t² = 1 - sin 2x; откуда sin 2x = 1 - t². Значит,

что равносильно следующим системам неравенств:

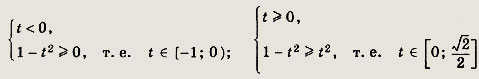
Следовательно,

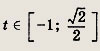
Теперь решаем неравенство

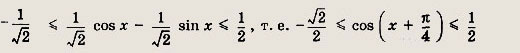
Получаем

Ответ:

Задание 331.

sin x sin 2х - cos х cos 2х > sin 6x

Ответ:

Задание 332.

Указание:

Замените

Ответ:

Задание 333.

Решение:

Функция у = arccos x определена на [-1; 1] и монотонно убывает на этом отрезке. При этом

Ответ:

Задание 334.

Ответ:

Задание 335.

arcsin x < arccos x

Указание:

Заменив

приведите неравенство к виду

Ответ:

Задание 336.

tg² (arcsin x) > 1

Указание:

Так как

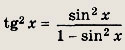
a sin (arcsin x) = x, то при х € (-1; 1) неравенство приводится к виду

Ответ:

Задание 337.

При каких а неравенство

a² + 2a - sin²x - 2a cos x > 2

выполняется для любого х € R?

Указание:

Сделав замену cos x = t, сведите задачу к следующей: найти значения а, при которых неравенство

t² - 2at + (а² - 2а - 3) > 0

выполнено для всех t € [-1; 1].

Ответ:

Задание 338.

Найдите все х, для которых выражение

(cos x + cos 5x)(2 sin x - 3 cos x + 4)

положительно.


Решение:

Так как

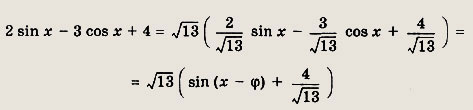
где

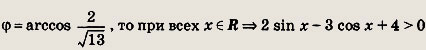
Поэтому исходное неравенство эквивалентно неравенству cos 5х + cos х > 0, т. е. 2 cos Зх cos 2х > 0. Нанесем на числовую ось нули функции у = cos Зх, т. е.

и функции

n, k € Z. Общий период обеих функций равен 2П, поэтому достаточно выяснить знак произведения

cos Зx cos 2x для х € [0; 2П].

Учитывая, что при переходе через каждую из отмеченных точек знак произведения меняется, получаем следующий ответ.

Ответ: