Границы применимости геометрической оптики. Если длина волны излучения много меньше линейных размеров тех объектов, с которыми взаимодействует свет ( l  << L ), то можно рассматривать свет как совокупность лучей, распространение которых подчиняется простым законам:

1.Лучи света распространяются прямолинейно.

2.Справедлив закон отражения.

3.Справедлив закон преломления.

При этих условиях можно не учитывать волновые свойства света (явления дифракции и интерференции).

Основные понятия геометрической оптики . Геометрическая оптика изучает изображения объектов, получаемые после прохождения отраженных от объекта лучей света через оптические устройства. Эти устройства могут быть двух типов: отражательные ( зеркал а) и преломляющие ( линзы ). Конечно, сложное оптическое устройство может быть произвольной комбинацией зеркал и линз.

Всякий предмет, изображение которого дает оптическое устройство, может быть представлен как совокупность светящихся точек, испускающих лучи света. Таким образом, чтобы в рамках геометрической оптики построить изображение предмета, следует понять, как распространяются отдельные лучи от точечных источников.

Ось симметрии оптического устройства, соединяющая точечный объект с центром кривизны зеркала или линзы, называется главной оптической осью . Геометрическая оптика рассматривает отображение пучка лучей, идущих вблизи от главной оптической оси (если это условие не выполнено, возникают отклонения от законов геометрической оптики - оптические аберрации ). Если изображение точки, находящейся над оптической осью, также находится над оптической осью, оно называется прямым . В противном случае изображение называется обратным . Увеличением оптического устройства m называется отношение размера изображения к размеру объекта, причем по соглашению увеличение считается положительным , если изображение прямое, и отрицательным - если изображение обратное.

Сферические зеркала.

Правила:

1. Расстояние до объекта s считается положительным, если объект находится на той же стороне относительно поверхности зеркала, что и падающий свет. В противном случае расстояние s считается отрицательным.

2. Расстояние до изображения s' считается положительным, если изображение находится на той же стороне зеркала, что и отраженный свет. Такое изображение называется действительным . В противном случае s' считается отрицательным, а изображение называется мнимым .

3. Радиус кривизны зеркала R положителен, если центр кривизны находится на той же стороне по отношению к поверхности зеркала, что и отраженный свет. В ином случае радиус кривизны отрицателен. Знак фокусного расстояния сферического зеркала f = R/2 определяется знаком R .

Применяя закон отражения света, можно вывести формулу сферического зеркала, связывающую расстояния от объекта и от изображения до зеркала с фокусным расстоянием или радиусом кривизны зеркала:

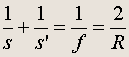(3.1)

Особенности хода главных лучей:

1. Луч, проходящий через центр кривизны зеркала, отражается назад.

2. Луч, проходящий через фокус зеркала, отражается и идет параллельно главной оптической оси.

3. Луч, идущий параллельно главной оптической оси, отражаясь от зеркала, проходит через фокус.

Формула для зеркала справедлива во всех случаях:

а)		- вогнутое зеркало; увеличение
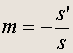(3.2)
б)		- выпуклое зеркало; изображение прямое и мнимое;
в)		- плоское зеркало.т.е. изображение обратное; В этом случае из формулы следует, что s' = - s . Так как изображение в плоском зеркале мнимое, то расстояние от зеркала до изображения следует считать отрицательным.
Поэтому увеличение

Линзы. Для того, чтобы можно было применять законы геометрической оптики к преломляющим линзам, эти линзы должны быть тонкими (в противном случае возникают сильные искажения изображения, обусловленные разностью хода лучей в разных частях линзы).

Два главных типа линз:

1. Собирающая линза, которая собирает падающий на нее пучок света, параллельный оптической оси, в одной точке по другую сторону линзы, называемой главным фокусом; расстояние от центра линзы до этой точки называется фокусным расстоянием  f > 0 ;

2. Рассеивающая линза, которая рассеивает падающий на нее пучок света, параллельный главной оптической оси так, что при продлении всех лучей они собираются в одной точке - фокусе, расположенном на той же стороне линзы, что и падающий пучок света; при этом фокусное расстояние f < 0 .

В отличие от зеркал, линзы имеют два фокуса по обе стороны линзы. Основная формула для линзы любого типа имеет тот же вид, что и для зеркала:

 

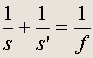
 Все соглашения о знаках величин s , s' f сохраняют силу, если только дополнить их условием, что s' > 0 , когда действительное изображение находится по другую сторону линзы. Увеличение линзы также определяется прежней формулой

 

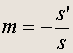
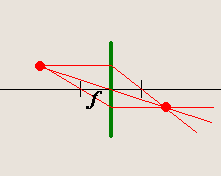
Особенности хода главных лучей в собирающей линзе:

1. Луч, проходящий через центр линзы, не искажается. 2.Луч, проходящий через передний фокус линзы (тот фокус, который находится по ту же сторону, что источник), идет после преломления параллельно главной оптической оси . 3.Луч, идущий параллельно главной оптической оси, после преломления проходит через задний фокус линзы.

 

Величина, обратная фокусному расстоянию линзы, называется оптической силой линзы D :

 

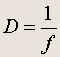
Размерность: [D] = диоптрия (дптр). Линза с фокусным расстоянием 1 м имеет оптическую силу 1 дптр.